Three Sort: An Efficient Hybrid Sorting Algorithm [AI Assisted Research - 2024 YR4 Mission]

Introduction

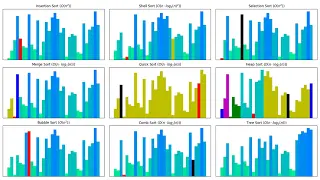
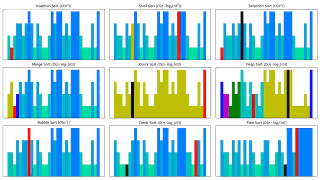
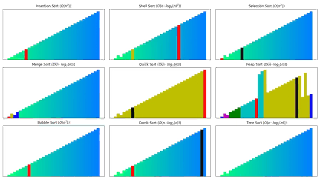
Algorithm Three Sort is a hybrid sorting algorithm developed by Oscar Riveros, designed to optimize performance across various data sizes and scenarios. It combines the strengths of Quicksort, known for its average-case efficiency, with Insertion Sort, which excels on small datasets due to excellent cache locality.

Explanation

Components:

1. Quicksort:

   • Pivot Selection: Uses a median-of-three method to choose a pivot, enhancing stability.
   • Partitioning: Rearranges elements around the pivot, creating subarrays that are recursively sorted.

2. Insertion Sort:

   • Applied on small subarrays determined by a threshold based on log2(mid) + 1, ensuring optimal performance on small datasets.

Process:

1. Initial Check: If the array segment is too small, Insertion Sort is used.
2. Pivot Selection: Chooses the median of three elements to reduce worst-case scenarios.
3. Partitioning: Elements are rearranged around the pivot, minimizing swaps and improving cache efficiency.
4. Recursive Sorting: Quicksort is applied recursively on subarrays until all segments meet the small size threshold.

Complexity Analysis

Time Complexity:

• Average Case: O(n log n) due to efficient partitioning in Quicksort.
• Worst Case: O(n^2), though mitigated by median-of-three pivot selection and hybrid approach.
• Best Case: O(n log n), achieved with balanced partitions.

Space Complexity:

• Recursive Calls: O(log n) for the recursion stack, efficient for typical use cases.

Implementation

The Python implementation integrates both sorting methods:

import math

def insertion_sort(lst, left, right):
    for i in range(left + 1, right + 1):
        key = lst[i]
        j = i - 1
        while j >= left and lst[j] > key:
            lst[j + 1] = lst[j]
            j -= 1
        lst[j + 1] = key

def tree_sort(lst, left, right):
    if left >= right:
        return
    
    mid = (left + right) // 2
    if mid != 0 and right - left + 1 <= math.log2(mid) + 1:  
        insertion_sort(lst, left, right)
        return

    # Median-of-three pivot selection
    pivot = lst[mid]
    
    # Swap pivot to end for partitioning
    lst[mid], lst[right] = lst[right], lst[mid]

    i, j = left - 1, right

    while True:
        i += 1
        while lst[i] < pivot:
            i += 1
        
        j -= 1
        while lst[j] > pivot:
            j -= 1
        
        if i >= j:
            break
        
        lst[i], lst[j] = lst[j], lst[i]
    
    # Swap pivot back to its correct position
    lst[right], lst[i] = lst[i], lst[right]

    tree_sort(lst, left, i - 1)
    tree_sort(lst, i + 1, right)

Example Usage:

lst = [3, 6, 8, 10, 1, 2, 1]
tree_sort(lst, 0, len(lst) - 1)
print(lst)  # Output: [1, 1, 2, 3, 6, 8, 10]

Conclusion

Algorithm Thee Sort excels in scenarios requiring efficient sorting with a hybrid approach. Its optimal use of Quicksort for larger datasets and Insertion Sort for small segments ensures good average performance while mitigating worst-case risks. Ideal for real-world applications where data size and stability are critical.