Graph Theory Reminder

This is intended to refresh these notions for those who have not played with them recently. It is also intended to specify the standards names used in the project and the library itself. As much as possible, QuickGraph naming convention follows the standard of graph theory naming.

Directed Graph, Vertex, Edges

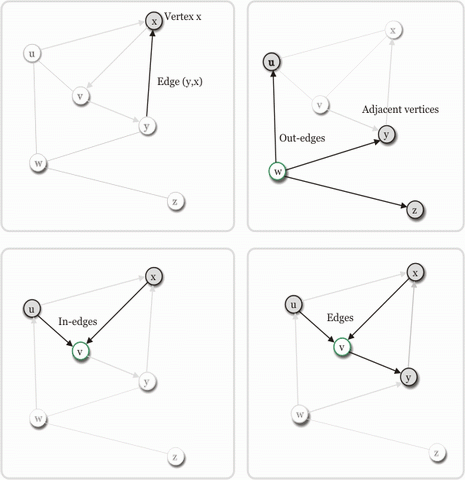
Let us start by redefining the basic concepts of directed graphs, vertices and edges. All these definitions are illustrated in the figure above.

• A directed graph G=(VxE) consists of a finite set V=V(G) of vertices and a finite multi-set E contained in VxV = {(u,v)| u,v in V} of edges that are ordered pair of vertices where u is called the source vertex and v the target vertex.

Tip:

• TVertex and TEdge are generic parameters in QuickGraph. The TEdge parameter has an additional constraint that it has to implement IEdge<TVertex>.

public interface IEdge<TVertex>
{
    TVertex Source {get;}
    TVertex Target { get;}
}

public interface ISomeGraphAlgorithm<TVertex,TEdge>
    where Edge : IEdge<TVertex>
{…}

• If e=(u,v), then e is an out-edge of u and an in-edge of v. in-degree(v) denotes the number of incoming edges of v and out-degree(u), the number of outgoing edges of u. The degree of u is the sum of its in-degree and out-degree.
• If a graph allows multiple edges from the same (u,v) vertex pair, it is called a multi-graph. Such edges are called parallel edges.
• A path from u to v is a sequence of edges e1,e2,...,en such that e1 source is u, en target is v and each edge in the sequence is an out-edge of it’s predecessor.
• A cycle is a path where the beginning vertex is equal to the end vertex.
• A directed acyclic graph (DAG) is a directed graph with no cycle.
• A weighted directed graph G:(VxExW) is a directed graph with an additional relation that associate each edge to a weight: e -> w(e) (for example, the distance).
• An adjacency graph is a data structure to represent a directed graph where the out-edges of any vertex can be accessed in amortized constant time.
• A bidirectional graph is a data structure to represent directed graph where both the out-edges and the in-edges of any vertex can be accessed in amortized constant time.
• QuickGraph also provides data structures for UndirectedGraph.

tip: The adjacency graph is implemented as a dictionary of Vertex to a collection of out-edges. When using a bidirectional graph, two dictionaries (one for in-edges, one for out-edges) have to be used, which doubles the required memory. Such data structures are most efficient for sparse graphs.