State Estimation

Step 1 - Noisy GPS and Accelerometer Data

Scenario 6

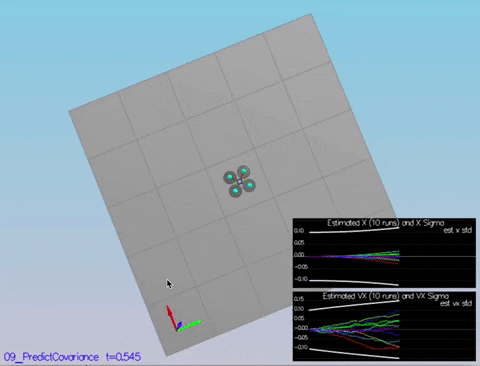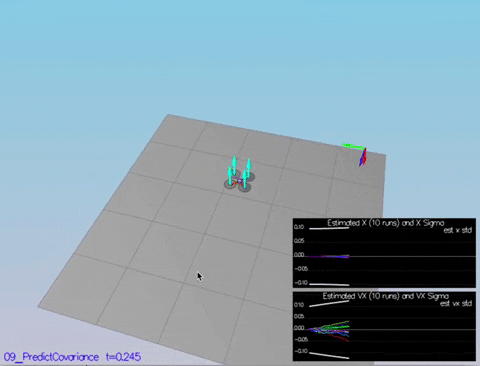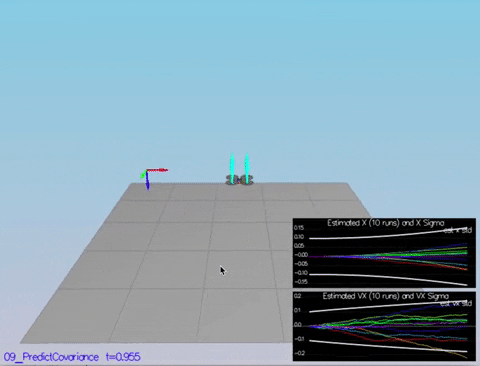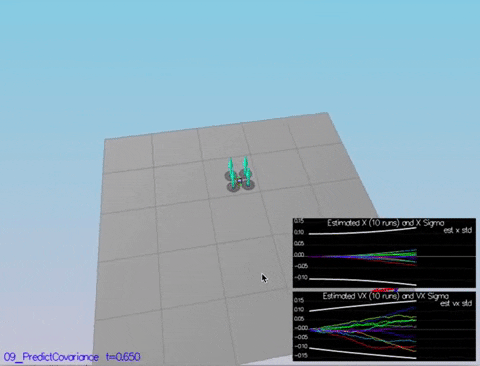
I loaded the gps and accelerometer logs into a Python Notebook here: https://app.mode.com/arush/reports/c676b4cb074b

import statistics
import numpy as np

gps = np.array(datasets[1].quad_gps_x)
accel = np.array(datasets[0].quad_imu_ax)

gps_s = statistics.stdev(gps)
accel_s = statistics.stdev(accel)
print('Accelerometer.X Sigma: {}'.format(accel_s))
print('GPS.X Sigma: {}'.format(gps_s))

Output

Accelerometer.X Sigma: 0.5120133550335954
GPS.X Sigma: 0.6918653080480083

Step 2 - Quaternion for attitude estimation using complementary filter

Scenario 7

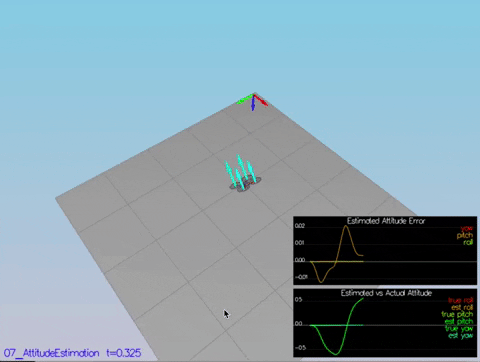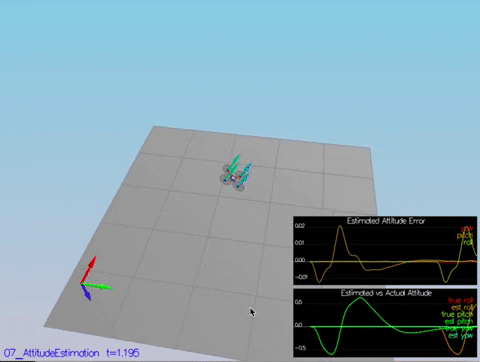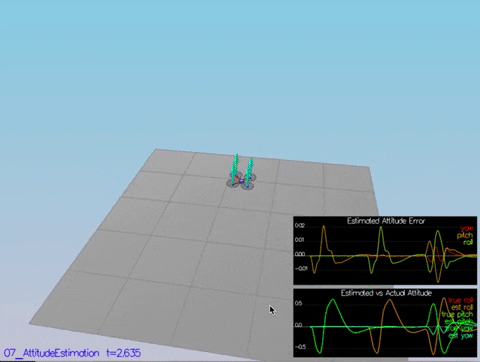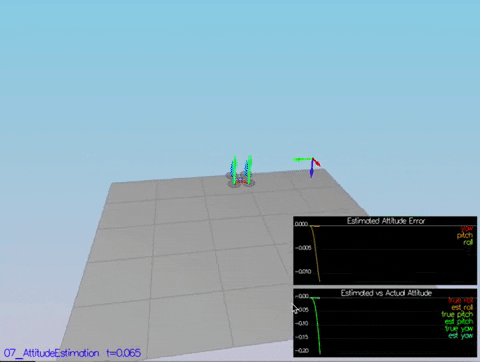
Here we're using a complementary filter for updating the roll and pitch, and just directly integrating yaw from gyro measurements.

I chose to use quaternions because it is a clean way to use body rates to do the integration in one LoC.

1. convert the estimate from Euler angles
2. integrate body rates with the quaternion in-place
3. convert estimate back to euler angles and update state ivar

// set quaternion with current estimated euler angles
Quaternion<float> qt = qt.FromEuler123_RPY(rollEst, pitchEst, ekfState(6));

// integrate body rate which basically multiplies pqr measurements with timestep
// projects the quaternion forward in time, doesn't change its type, i.e. still a Quaternion<float>
qt.IntegrateBodyRate((V3D)gyro, (double)dtIMU);

// back to euler
V3D predictedRPY = qt.ToEulerRPY();
float predictedRoll = predictedRPY.x;
float predictedPitch = predictedRPY.y;
ekfState(6) = (float)predictedRPY.z; // yaw

Step 3 - Prediciton Step

Scenario 8 - Predict()

Here we use a basic integration to propagate the position and velocity forward with the acceleration and add in gravity.

predictedState(0) += curState(3) * dt;
predictedState(1) += curState(4) * dt;
predictedState(2) += curState(5) * dt;

// attitude.Rotate_BtoI(<V3F>) to rotate a vector from body frame to inertial frame
const V3F acc_inertial = attitude.Rotate_BtoI(accel) - V3F(0.0F, 0.0F, CONST_GRAVITY);

// predict x_dot, y_dot, z_dot
predictedState(3) += acc_inertial.x * dt;
predictedState(4) += acc_inertial.y * dt;
predictedState(5) += acc_inertial.z * dt;

Scenario 9 - Jacobians

First we implement GetRgbPrime as per the following equation

like this

float theta = pitch;
float phi = roll;
float psi = yaw;

RbgPrime(0,0) = -cos(theta) * sin(psi);
RbgPrime(0,1) = -sin(phi) * sin(theta) * sin(psi) - cos(phi) * cos(psi);
RbgPrime(0,2) = -cos(phi) * sin(theta) * sin(psi) + sin(phi) * cos(psi);

RbgPrime(1,0) = cos(theta) * cos(psi);
RbgPrime(1,1) = sin(phi) * sin(theta) * cos(psi) - cos(phi) * sin(psi);
RbgPrime(1,2) = cos(phi) * sin(theta) * cos(psi) + sin(phi) * sin(psi);

RbgPrime(2,0) = 0;
RbgPrime(2,1) = 0;
RbgPrime(2,2) = 0;

and then plug in the values into the Jacobian

like this

MatrixXf gPrime(QUAD_EKF_NUM_STATES, QUAD_EKF_NUM_STATES);
gPrime.setIdentity();

gPrime(0, 3) = dt;
gPrime(1, 4) = dt;
gPrime(2, 5) = dt;

// control input is just acceleration
gPrime(3, 6) = (RbgPrime(0) * accel).sum() * dt;
gPrime(4, 6) = (RbgPrime(1) * accel).sum() * dt;
gPrime(5, 6) = (RbgPrime(2) * accel).sum() * dt;

ekfCov = gPrime * ekfCov * gPrime.transpose() + Q;

Scenario 10 - Magenetometer Update

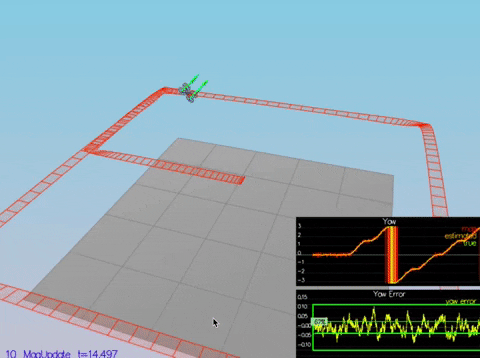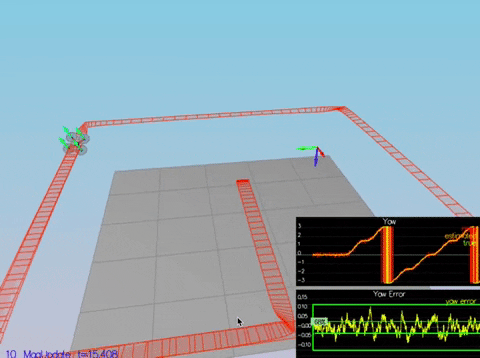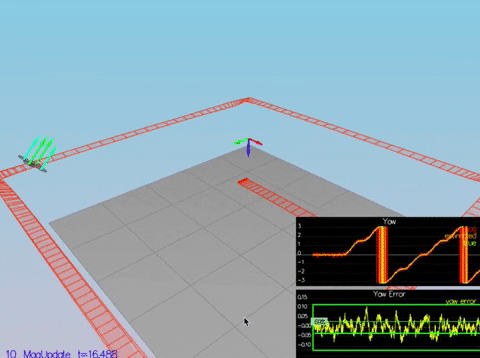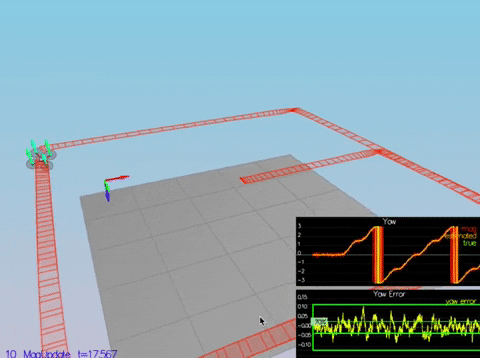
We simply implement the mag update formula here:

Section 7.3.2 dictates

hPrime(6) = 1;

// zFromX means estimated yaw (z) from state vector X
zFromX(0) = ekfState(6);

float diff = magYaw - zFromX(0);

// normalize
if (diff > F_PI) zFromX(0) += 2.f*F_PI;
if (diff < -F_PI) zFromX(0) -= 2.f*F_PI;

Update(z, hPrime, R_Mag, zFromX);

Scenario 11 - GPS

Here is the formula for GPS updates

// The measurement z for the GPS is [x, y, z, x_dot, y_dot, z_dot] and the measurement model is h(xt) = [xt.x, xt.y xt.z, xt.x_dot, xt.y_dot, xt.z_dot].
hPrime(0, 0) = 1;
hPrime(1, 1) = 1;
hPrime(2, 2) = 1;
hPrime(3, 3) = 1;
hPrime(4, 4) = 1;
hPrime(5, 5) = 1;

zFromX(0) = ekfState(0);
zFromX(1) = ekfState(1);
zFromX(2) = ekfState(2);
zFromX(3) = ekfState(3);
zFromX(4) = ekfState(4);
zFromX(5) = ekfState(5);

Update(z, hPrime, R_GPS, zFromX);

Scenario 11 - With own controller code

PASS: ABS(Quad.Est.E.Pos) was less than 1.000000 for at least 20.000000 seconds

The test passes but the path is supposed to be wonky because its using simulated GPS data.