Skip to content

Latest commit

 

History

History
304 lines (247 loc) · 8.8 KB

README.md

File metadata and controls

304 lines (247 loc) · 8.8 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1603
第 419 场周赛 Q2
树
深度优先搜索
二叉树
排序

3319. 第 K 大的完美二叉子树的大小

English Version

题目描述

给你一棵 二叉树 的根节点 root 和一个整数k。

返回第 k 大的 完美二叉子树 的大小，如果不存在则返回 -1。

完美二叉树 是指所有叶子节点都在同一层级的树，且每个父节点恰有两个子节点。

 

示例 1：

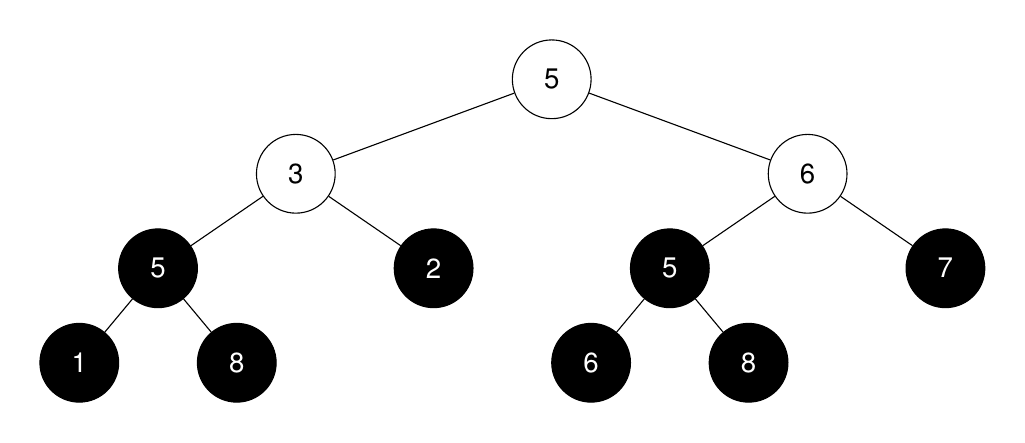
输入： root = [5,3,6,5,2,5,7,1,8,null,null,6,8], k = 2

输出： 3

解释：

完美二叉子树的根节点在图中以黑色突出显示。它们的大小按非递增顺序排列为 [3, 3, 1, 1, 1, 1, 1, 1]。
第 2 大的完美二叉子树的大小是 3。

示例 2：

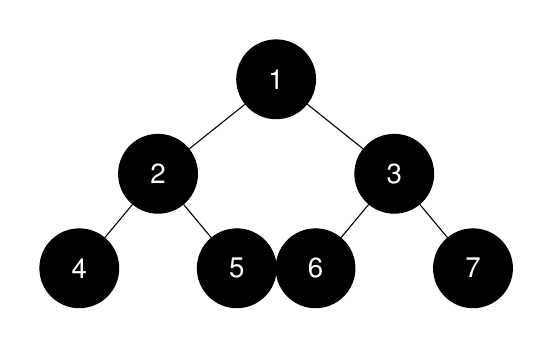
输入： root = [1,2,3,4,5,6,7], k = 1

输出： 7

解释：

完美二叉子树的大小按非递增顺序排列为 [7, 3, 3, 1, 1, 1, 1]。最大的完美二叉子树的大小是 7。

示例 3：

输入： root = [1,2,3,null,4], k = 3

输出： -1

解释：

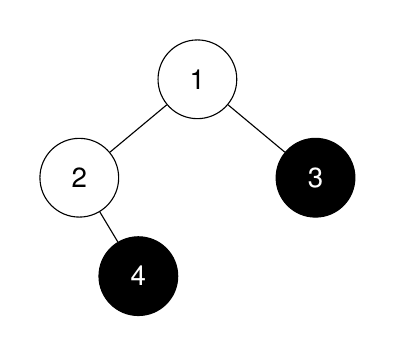
完美二叉子树的大小按非递增顺序排列为 [1, 1]。完美二叉子树的数量少于 3。

 

提示：

  • 树中的节点数目在 [1, 2000] 范围内。
  • 1 <= Node.val <= 2000
  • 1 <= k <= 1024

解法

方法一：DFS + 排序

我们定义一个函数 $\textit{dfs}$，用于计算以当前节点为根节点的完美二叉子树的大小，用一个数组 $\textit{nums}$ 记录所有完美二叉子树的大小。如果以当前节点为根节点的子树不是完美二叉子树，则返回 $-1$。

函数 $\textit{dfs}$ 的执行过程如下：

  1. 如果当前节点为空，则返回 $0$；
  2. 递归计算左子树和右子树的完美二叉子树的大小，分别记为 $l$ 和 $r$；
  3. 如果左子树和右子树的大小不相等，或者左子树和右子树的大小小于 $0$，则返回 $-1$；
  4. 计算当前节点的完美二叉子树的大小 $\textit{cnt} = l + r + 1$，并将 $\textit{cnt}$ 添加到数组 $\textit{nums}$ 中；
  5. 返回 $\textit{cnt}$。

我们调用 $\textit{dfs}$ 函数计算出所有完美二叉子树的大小，如果数组 $\textit{nums}$ 的长度小于 $k$，则返回 $-1$，否则对数组 $\textit{nums}$ 进行降序排序，返回第 $k$ 大的完美二叉子树的大小。

时间复杂度 $O(n \times \log n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthLargestPerfectSubtree(self, root: Optional[TreeNode], k: int) -> int:
        def dfs(root: Optional[TreeNode]) -> int:
            if root is None:
                return 0
            l, r = dfs(root.left), dfs(root.right)
            if l < 0 or l != r:
                return -1
            cnt = l + r + 1
            nums.append(cnt)
            return cnt

        nums = []
        dfs(root)
        if len(nums) < k:
            return -1
        nums.sort(reverse=True)
        return nums[k - 1]

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<Integer> nums = new ArrayList<>();

    public int kthLargestPerfectSubtree(TreeNode root, int k) {
        dfs(root);
        if (nums.size() < k) {
            return -1;
        }
        nums.sort(Comparator.reverseOrder());
        return nums.get(k - 1);
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int l = dfs(root.left);
        int r = dfs(root.right);
        if (l < 0 || l != r) {
            return -1;
        }
        int cnt = l + r + 1;
        nums.add(cnt);
        return cnt;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthLargestPerfectSubtree(TreeNode* root, int k) {
        vector<int> nums;
        auto dfs = [&](auto&& dfs, TreeNode* root) -> int {
            if (!root) {
                return 0;
            }
            int l = dfs(dfs, root->left);
            int r = dfs(dfs, root->right);
            if (l < 0 || l != r) {
                return -1;
            }
            int cnt = l + r + 1;
            nums.push_back(cnt);
            return cnt;
        };
        dfs(dfs, root);
        if (nums.size() < k) {
            return -1;
        }
        ranges::sort(nums, greater<int>());
        return nums[k - 1];
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func kthLargestPerfectSubtree(root *TreeNode, k int) int {
	nums := []int{}
	var dfs func(*TreeNode) int
	dfs = func(root *TreeNode) int {
		if root == nil {
			return 0
		}
		l, r := dfs(root.Left), dfs(root.Right)
		if l < 0 || l != r {
			return -1
		}
		cnt := l + r + 1
		nums = append(nums, cnt)
		return cnt
	}
	dfs(root)
	if len(nums) < k {
		return -1
	}
	sort.Sort(sort.Reverse(sort.IntSlice(nums)))
	return nums[k-1]
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function kthLargestPerfectSubtree(root: TreeNode | null, k: number): number {
    const nums: number[] = [];
    const dfs = (root: TreeNode | null): number => {
        if (!root) {
            return 0;
        }
        const l = dfs(root.left);
        const r = dfs(root.right);
        if (l < 0 || l !== r) {
            return -1;
        }
        const cnt = l + r + 1;
        nums.push(cnt);
        return cnt;
    };
    dfs(root);
    if (nums.length < k) {
        return -1;
    }
    return nums.sort((a, b) => b - a)[k - 1];
}