(1) illustrating attention, NMT in https://www.tensorflow.org/text/tutorials/nmt_with_attention
the generated attention plot is perhaps more interesting shows which parts of the input sentence has the model's attention while translating
(2) introduction, attention-mechanism.py see https://machinelearningmastery.com/the-attention-mechanism-from-scratch/
"Within the context of machine translation, each word in an input sentence would be attributed its own query, key and value vectors. These vectors are generated by multiplying the encoder’s representation of the specific word under consideration, with three different weight matrices that would have been generated during training.
In essence, when the generalized attention mechanism is presented with a sequence of words, it takes the query vector attributed to some specific word in the sequence and scores it against each key in the database. In doing so, it captures how the word under consideration relates to the others in the sequence. Then it scales the values according to the attention weights (computed from the scores), in order to retain focus on those words that are relevant to the query. In doing so, it produces an attention output for the word under consideration."
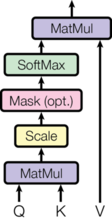
(3) attention mechanism in Attention is all you need https://arxiv.org/abs/1706.03762 (transformers)
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
We call our particular attention “Scaled Dot-Product Attention”. The input consists of queries and keys of dimension , and values of dimension
.
We compute the dot products of the query with all keys, divide each by
, and apply a softmax function to obtain the weights on the values.
pytorch implementation would be
def attention(query, key, value, mask=None, dropout=None):
"Compute 'Scaled Dot Product Attention'"
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
In practice, we compute the attention function on a set of queries
simultaneously, packed together into a matrix . The keys and values are
also packed together into matrices
and
. We compute the matrix of
outputs as:
most common attention functions
The two most commonly used attention functions are additive attention
(cite), and dot-product (multiplicative)
attention. Dot-product attention is identical to our algorithm, except for the
scaling factor of . Additive attention computes the
compatibility function using a feed-forward network with a single hidden layer.
While the two are similar in theoretical complexity, dot-product attention is
much faster and more space-efficient in practice, since it can be implemented
using highly optimized matrix multiplication code.
While for small values of the two mechanisms perform similarly, additive
attention outperforms dot product attention without scaling for larger values of
(cite). We suspect that for large
values of
, the dot products grow large in magnitude, pushing the softmax
function into regions where it has extremely small gradients (To illustrate why
the dot products get large, assume that the components of
and
are
independent random variables with mean 0 and variance 1. Then their dot
product,
, has mean 1 and variance
.). To counteract this effect, we scale the dot products by
.
about multi-head attention
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.
a pytorch implementation
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
"Take in model size and number of heads."
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
"Implements Figure 2"
if mask is not None:
# Same mask applied to all h heads.
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) Do all the linear projections in batch from d_model => h x d_k
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) Apply attention on all the projected vectors in batch.
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) "Concat" using a view and apply a final linear.
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
where
Where the projections are parameter matrices ,
,
.
In this work we employ 8 parallel attention layers, or heads. For each of
these we use . Due to the reduced dimension of
each head, the total computational cost is similar to that of single-head
attention with full dimensionality.
application of multihead attention in transformers
The Transformer uses multi-head attention in three different ways:
-
In “encoder-decoder attention” layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence. This mimics the typical encoder-decoder attention mechanisms in sequence-to-sequence models such as (cite).
-
The encoder contains self-attention layers. In a self-attention layer all of the keys, values and queries come from the same place, in this case, the output of the previous layer in the encoder. Each position in the encoder can attend to all positions in the previous layer of the encoder.
-
Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot- product attention by masking out (setting to
) all values in the input of the softmax which correspond to illegal connections.
(4) neural machine translation with attention https://www.tensorflow.org/text/tutorials/nmt_with_attention
overview of the model, at each time-step the decoder's output is combined with a weighted sum over the encoded input, to predict the next word, the diagram and formulas are from Luong's paper : https://arxiv.org/abs/1508.04025v5
The decoder uses attention to selectively focus on parts of the input sequence, the attention takes a sequence of vectors as input for each example and returns an "attention" vector for each example. This attention layer is similar to a layers.GlobalAveragePoling1D but the attention layer performs a weighted average.
how the decoder works
the decoder's job is to generate predictions for the next output token.
1.The decoder receives the complete encoder output.
2.It uses an RNN to keep track of what it has generated so far.
3.It uses its RNN output as the query to the attention over the encoder's output, producing the context vector.
4.It combines the RNN output and the context vector using Equation 3 (below) to generate the "attention vector".
5.It generates logit predictions for the next token based on the "attention vector".