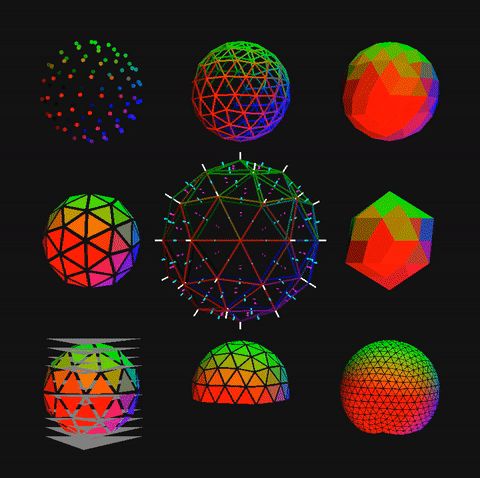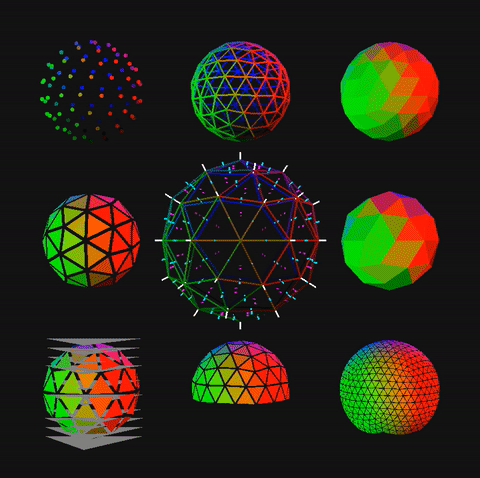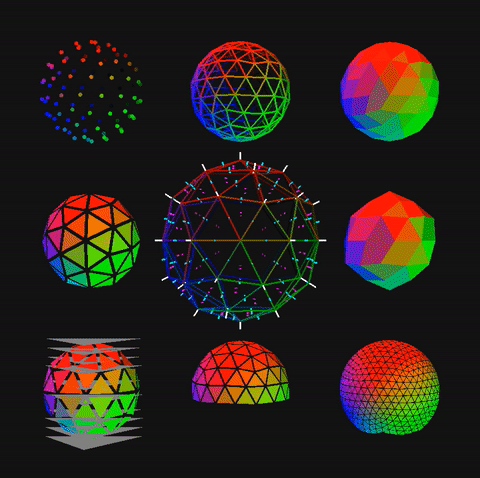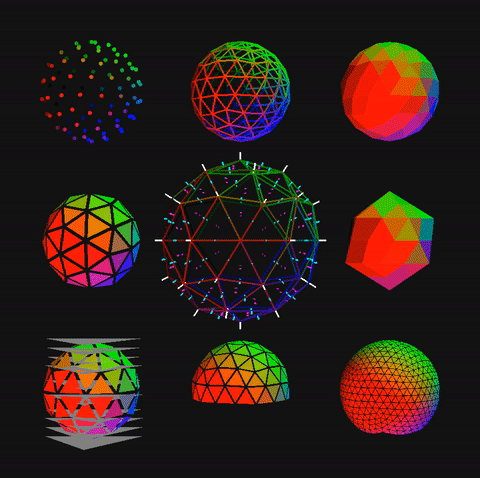R. Buckminster Fuller method 1 spheres and domes from icosahedra or octahedra
make then make run
geodesic.h + .cdataOpenGL/mesh.h + .crendering, and more mesh data for rendering
// sphere
geodesicSphere icosahedronSphere(int v);
geodesicSphere octahedronSphere(int v);
geodesicSphere tetrahedronSphere(int v);
// dome
geodesicDome icosahedronDome(int v, float crop);
geodesicDome octahedronDome(int v, float crop);
geodesicDome tetrahedronDome(int v, float crop);geodesicSphere icosphere = icosahedron(3) // 3v icosahedron
geodesicDome dome = icosahedronDome(3, 5/9); // 3v 5/9 domenow you have access to points, lines, face, as well as normals data. For domes, there's also more complicated data involved in slicing the sphere into a dome including number of slice meridians, triangle count on each row, relationship of face to row number.
geodesicMeshTriangles mesh = makeMeshTriangles(&icosphere, .75){
geodesicMeshNormals normals = makeMeshNormals(&icosphere);// draw geodesic objects
drawGeodesicTriangles(&icosphere);
drawDomeMeshTriangles(&dome, &domeTriangleMesh);
// draw mesh objects
drawGeodesicExtrudedTriangles(&mesh);
drawGeodesicVertexNormalLines(&normals);
drawGeodesicFaceNormalLines(&normals);delete geometry when you are done
deleteGeodesicSphere(&geodesic);
deleteGeodesicDome(&dome);
deleteMeshNormals(&normals);
deleteMeshTriangles(&mesh);