1254

1254. Number of Closed Islands (Medium)

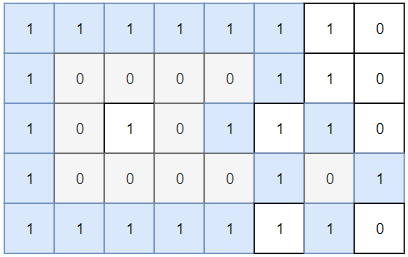
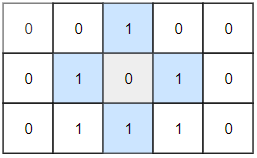
Given a 2D grid consists of 0s (land) and 1s (water).  An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

 

Example 1:

Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

 

Constraints:

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

Related Topics:
Depth-first Search

Solution 1. DFS

// OJ: https://leetcode.com/problems/number-of-closed-islands/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(1)
class Solution {
    int dirs[4][2] = {{0,1},{0,-1},{-1,0},{1,0}}, M, N;
    bool dfs(vector<vector<int>> &G, int x, int y, int id) {
        G[x][y] = id;
        bool ans = true;
        for (auto &[dx, dy] : dirs) {
            int a = x + dx, b = y + dy;
            bool oob = a < 0 || b < 0 || a >= M || b >= N;
            ans = ans && !oob;
            if (oob || G[a][b] != 0) continue;
            ans = dfs(G, a, b, id) && ans;
        }
        return ans;
    }
public:
    int closedIsland(vector<vector<int>>& G) {
        int id = 2, ans = 0;
        M = G.size(), N = G[0].size();
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                if (G[i][j] != 0) continue;
                if (dfs(G, i, j, id++)) ++ans;
            }
        }
        return ans;
    }
};