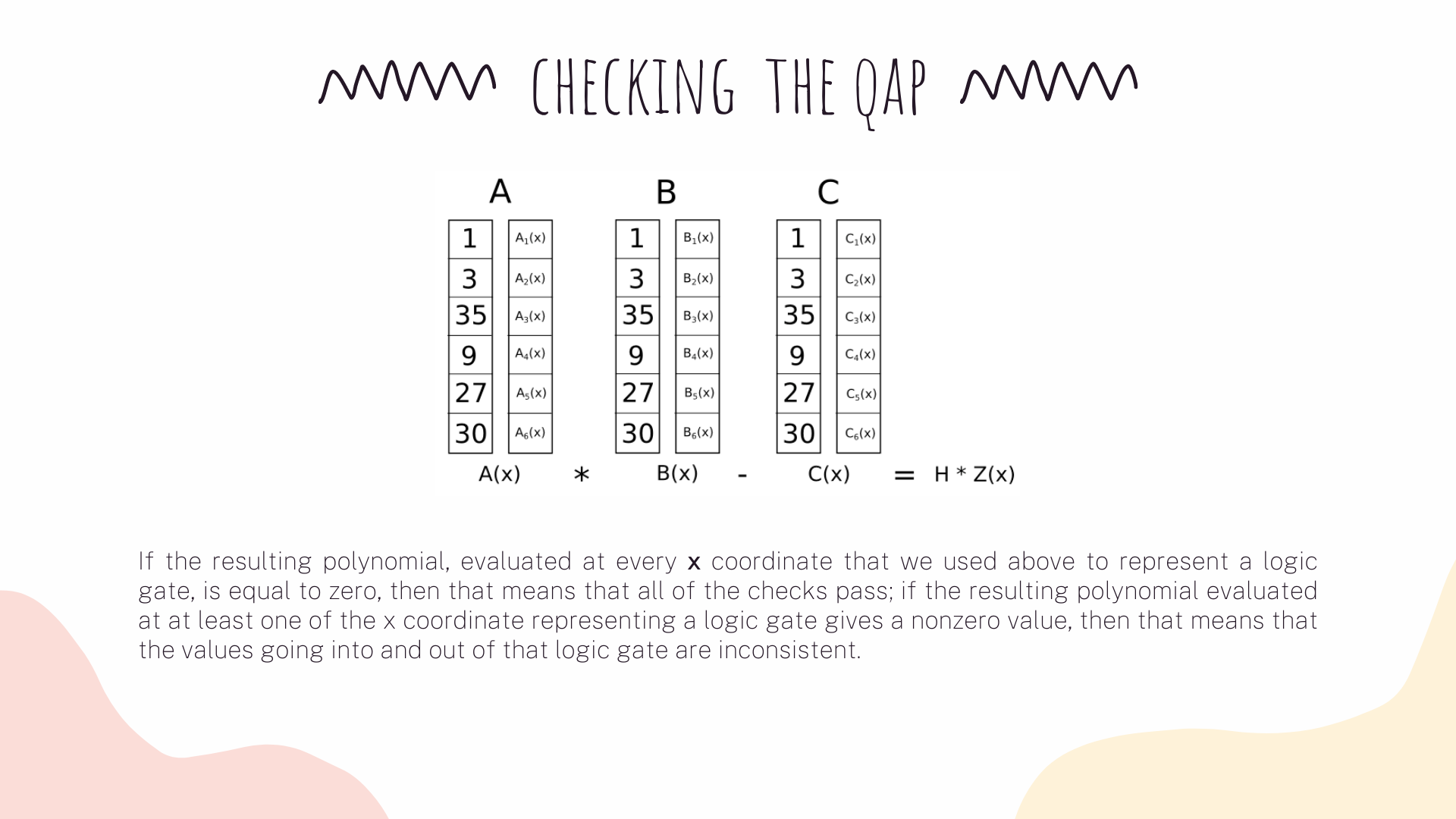
Once that we have the QAP from our R1CS, we can chek all the constraints at the same time by doing the dot product check on the polynomials. Because in this case the dot product check is a series of additions and multiplications of polynomials, the result is itself going to be a polynomial. As follows:
And so we have the solution for the QAP. If we try to falsify any of the variables in the R1CS solution that we are deriving this QAP solution from — say, set the last one to 31 instead of 30, then we get a t polynomial that fails one of the checks, and furthermore t would not be a multiple of Z; rather, dividing t / Z would give a remainder of [-5.0, 8.833, -4.5, 0.666].
That's all for this thread. Thank you for reading! If you liked, follow me @Hasseru and retweet.