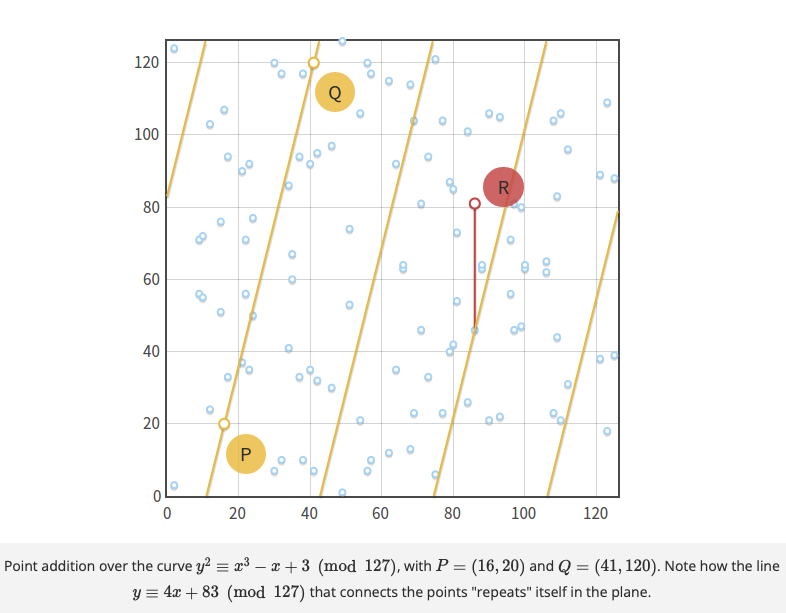
Today we are going to leard how the definition of addition change to work in a finite field. We can say that three points are aligned if there's a line that connects all of them. But lines if a finite field are not the same as lines in real field.
For example:
Given that we are in a group, point addition retains the properties we already know:
The equations for calculating point additions are exactly the same as in real field, except for the fact that we need to add "mod p" at the end of every expression.
That's all for this thread. Thank you for reading! If you liked this thread, follow me @Hasseru and retweet.