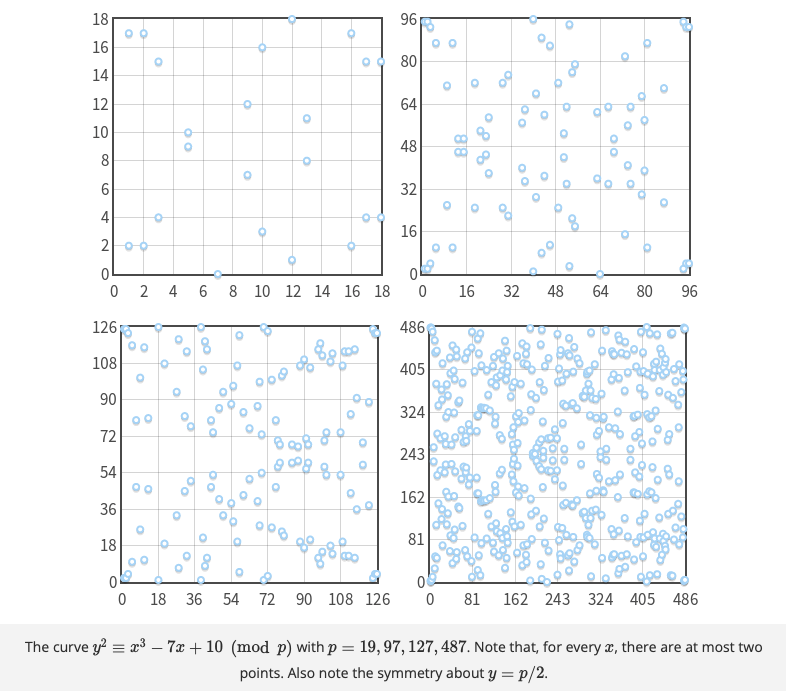
Today we are going to define how elliptic curve works over a finite field. Let’s remember that when we use modular math, we consider a set Zn, this is the finite field or the set of integers module p.
The set of points that are described by the equation of a elliptic curve and the point at inifinity, now becomes a set of points where a and b are two integers that belong to Zn. Mathematically, is described as follows:
What previously was a continuous curve is now a set of disjoint points in the xy-plane. But even if we have restricted our domain, elliptic curves in an finite field still form an abelian group. For example:
Clearly, we need to change a bit our definition of addition in order to make it work in a finite field. With reals, we said that the sum of three aligned points was zero (P + Q + R = 0). We can keep this definition, but what does it mean for three points to be aligned in a finite field? Tomorrow we are going to talk about this.
That's all for this thread. Thank you for reading! If you liked this thread, follow me @Hasseru and retweet.