ZKP is not a new concept and in order to understand ZKP there are a series of mathematics and cryptographic that need to be understood. So, we are going to spend some days learning about these concepts.
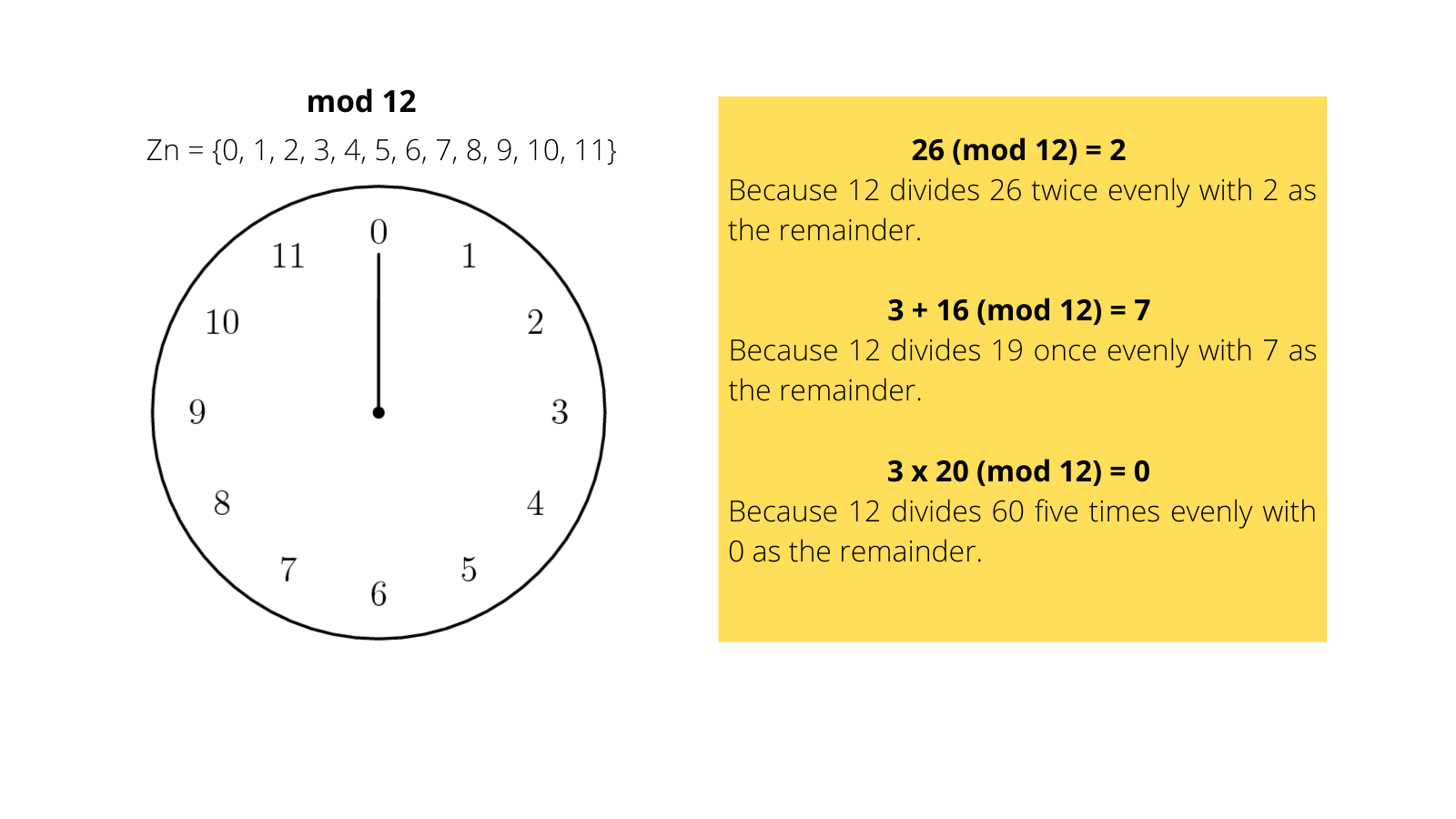
Modular math is a fundamental component of cryptographic. The idea is essentially very simple and is identical to the “clock arithmetic” you learn in school. More formally, Let n be a positive integer. We denote the set [0..n−1] by Zn.
We consider two integers "x","y" to be the same if "x" and "y" differ by a multiple of n, mathematically we write this as x=y(mod n) and we say that "x" and "y" are congruent module n. We may omit (mod n) when it is clear from context. Every integer "x" is congruent to some "y" in Zn. When we add or subtract multiples of n from an integer x to reach some y ∈ Zn, we say are reducing x module n, and y is the residue. For example:
Why modular arithmetic is important in cryptography?
Cryptographic operations are often done with fixed key length. While some operations can be done using any bit string of given length, others, especially public key operations are done over finite fields. Since, general arithmetic operations are not bounded within the domain, modular operations are used. It is just the same operation but reduced into a remainder when divided by a fixed modulo.
That's all for this thread. Thank you for reading! If you liked this thread, follow me @Hasseru and retweet.