README_CN.md

1971. 寻找图中是否存在路径

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 start 开始，到顶点 end 结束的 有效路径 。

给你数组 edges 和整数 n、start和end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1:

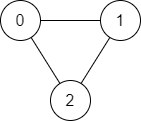
输入: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出: true
解释: 存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2
- 0 → 2

示例 2:

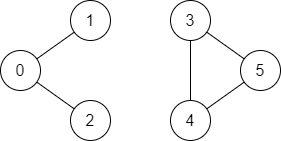
输入: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出: false
解释: 不存在由顶点 0 到顶点 5 的路径.

提示:

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• 不存在双向边
• 不存在指向顶点自身的边

题解 (Python)

1. 题解

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        paths = {}
        nodes = [source]
        seen = {source}

        for u, v in edges:
            if u not in paths:
                paths[u] = []
            if v not in paths:
                paths[v] = []
            paths[u].append(v)
            paths[v].append(u)

        while nodes:
            node0 = nodes.pop()
            for node1 in paths.get(node0, [node0]):
                if node1 == destination:
                    return True

                if node1 not in seen:
                    nodes.append(node1)
                    seen.add(node1)

        return False