README_CN.md

1610. 可见点的最大数目

给你一个点数组 points 和一个表示角度的整数 angle ，你的位置是 location ，其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。

最开始，你面向东方进行观测。你 不能 进行移动改变位置，但可以通过 自转 调整观测角度。换句话说，posx 和 posy 不能改变。你的视野范围的角度用 angle 表示， 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数，那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。

对于每个点，如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ，那么你就可以看到它。

同一个坐标上可以有多个点。你所在的位置也可能存在一些点，但不管你的怎么旋转，总是可以看到这些点。同时，点不会阻碍你看到其他点。

返回你能看到的点的最大数目。

示例 1:

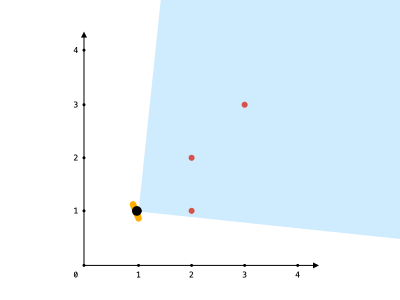
输入: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出: 3
解释: 阴影区域代表你的视野。在你的视野中，所有的点都清晰可见，尽管 [2,2] 和 [3,3]在同一条直线上，你仍然可以看到 [3,3] 。

示例 2:

输入: points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出: 4
解释: 在你的视野中，所有的点都清晰可见，包括你所在位置的那个点。

示例 3:

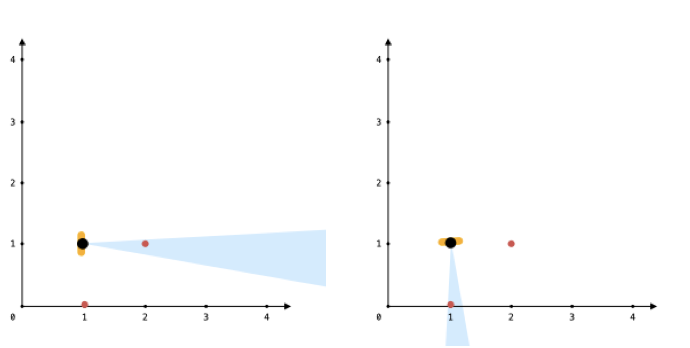
输入: points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出: 1
解释: 如图所示，你只能看到两点之一。

Constraints:

• 1 <= points.length <= 105
• points[i].length == 2
• location.length == 2
• 0 <= angle < 360
• 0 <= posx, posy, xi, yi <= 100

题解 (Rust)

1. 题解

impl Solution {
    pub fn visible_points(points: Vec<Vec<i32>>, angle: i32, location: Vec<i32>) -> i32 {
        let angle = (angle as f64).to_radians();
        let origin = points.iter().filter(|&p| *p == location).count();
        let mut points = points
            .iter()
            .filter(|&p| *p != location)
            .map(|p| ((p[1] - location[1]) as f64).atan2((p[0] - location[0]) as f64))
            .collect::<Vec<_>>();
        let mut i = 0;
        let mut max_count = 0;

        points.sort_unstable_by(|a, b| a.partial_cmp(b).unwrap());

        for j in 0..points.len() {
            points.push(points[j] + 2.0 * std::f64::consts::PI);
        }

        for j in 0..points.len() / 2 {
            while i < points.len() && points[i] - points[j] <= angle {
                i += 1;
            }

            max_count = max_count.max(i - j);
        }

        (origin + max_count) as i32
    }
}