README_CN.md

1514. 概率最大的路径

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1:

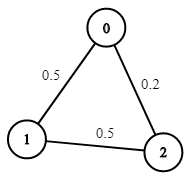
输入: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出: 0.25000
解释: 从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

示例 2:

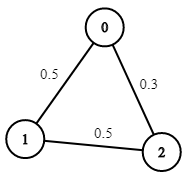
输入: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出: 0.30000

示例 3:

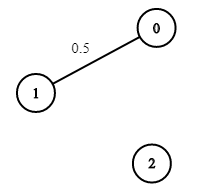
输入: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出: 0.00000
解释: 节点 0 和 节点 2 之间不存在路径

提示:

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• 每两个节点之间最多有一条边

题解 (Python)

1. 题解

import heapq


class Solution:
    def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start_node: int, end_node: int) -> float:
        graph = {start_node: [(1, start_node)]}
        seen = set()
        heap = [(-1, start_node)]
        heapq.heapify(heap)

        for i in range(len(edges)):
            if edges[i][0] not in graph:
                graph[edges[i][0]] = []
            if edges[i][1] not in graph:
                graph[edges[i][1]] = []
            graph[edges[i][0]].append((succProb[i], edges[i][1]))
            graph[edges[i][1]].append((succProb[i], edges[i][0]))

        while len(heap) > 0:
            prob0, node0 = heapq.heappop(heap)
            seen.add(node0)

            if node0 == end_node:
                return -prob0

            for prob1, node1 in graph[node0]:
                if node1 not in seen:
                    heapq.heappush(heap, (prob0 * prob1, node1))

        return 0