README_CN.md

1373. 二叉搜索子树的最大键值和

给你一棵以 root 为根的 二叉树 ，请你返回 任意 二叉搜索子树的最大键值和。

二叉搜索树的定义如下：

• 任意节点的左子树中的键值都 小于 此节点的键值。
• 任意节点的右子树中的键值都 大于 此节点的键值。
• 任意节点的左子树和右子树都是二叉搜索树。

示例 1:

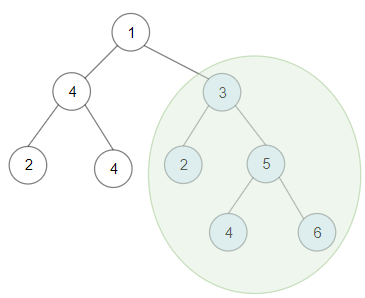
输入: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出: 20
解释: 键值为 3 的子树是和最大的二叉搜索树。

示例 2:

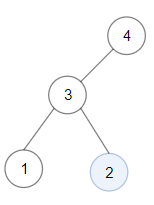
输入: root = [4,3,null,1,2]
输出: 2
解释: 键值为 2 的单节点子树是和最大的二叉搜索树。

示例 3:

输入: root = [-4,-2,-5]
输出: 0
解释: 所有节点键值都为负数，和最大的二叉搜索树为空。

示例 4:

输入: root = [2,1,3]
输出: 6

示例 5:

输入: root = [5,4,8,3,null,6,3]
输出: 7

提示:

• 每棵树有 1 到 40000 个节点。
• 每个节点的键值在 [-4 * 10^4 , 4 * 10^4] 之间。

题解 (Python)

1. 题解

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxSumBST(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> (bool, int, int, int, int):
            if root is None:
                return (True, 40001, -40001, 0, 0)

            isbstl, minl, maxl, suml, retl = dfs(root.left)
            isbstr, minr, maxr, sumr, retr = dfs(root.right)
            isbstt = isbstl and isbstr and root.val > maxl and root.val < minr

            if isbstt:
                sumt = suml + sumr + root.val
                return (True, min(minl, root.val), max(maxr, root.val), sumt, max(sumt, retl, retr))
            else:
                return (False, 0, 0, 0, max(retl, retr))

        return dfs(root)[4]