README_CN.md

1289. 下降路径最小和 II

给你一个 n x n 整数矩阵 grid ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 grid 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1:

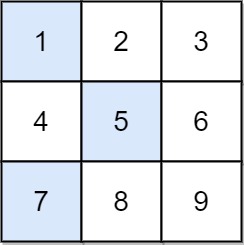
输入: grid = [[1,2,3],[4,5,6],[7,8,9]]
输出: 13
解释:
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2:

输入: grid = [[7]]
输出: 7

提示:

• n == grid.length == grid[i].length
• 1 <= n <= 200
• -99 <= grid[i][j] <= 99

题解 (Rust)

1. 题解

impl Solution {
    pub fn min_falling_path_sum(mut grid: Vec<Vec<i32>>) -> i32 {
        if grid.len() == 1 {
            return grid[0][0];
        }

        let mut min_col2 = [grid.len(); 2];
        let mut min_sum2 = [0; 2];

        for r in 0..grid.len() {
            let mut i = grid.len();
            let mut j = grid.len();

            for c in 0..grid.len() {
                if c != min_col2[0] {
                    grid[r][c] += min_sum2[0];
                } else {
                    grid[r][c] += min_sum2[1];
                }

                if grid[r][c] <= *grid[r].get(i).unwrap_or(&i32::MAX) {
                    j = i;
                    i = c;
                } else if grid[r][c] < *grid[r].get(j).unwrap_or(&i32::MAX) {
                    j = c;
                }
            }

            min_col2 = [i, j];
            min_sum2 = [grid[r][i], grid[r][j]];
        }

        min_sum2[0].min(min_sum2[1])
    }
}