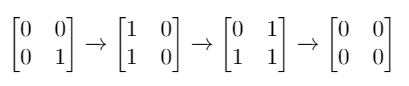README_CN.md

1284. 转化为全零矩阵的最少反转次数

给你一个 m x n 的二进制矩阵 mat。每一步，你可以选择一个单元格并将它反转（反转表示 0 变 1 ，1 变 0 ）。如果存在和它相邻的单元格，那么这些相邻的单元格也会被反转。相邻的两个单元格共享同一条边。

请你返回将矩阵 mat 转化为全零矩阵的最少反转次数，如果无法转化为全零矩阵，请返回 -1 。

二进制矩阵 的每一个格子要么是 0 要么是 1 。

全零矩阵 是所有格子都为 0 的矩阵。

示例 1:

输入: mat = [[0,0],[0,1]]
输出: 3
解释: 一个可能的解是反转 (1, 0)，然后 (0, 1) ，最后是 (1, 1) 。

示例 2:

输入: mat = [[0]]
输出: 0
解释: 给出的矩阵是全零矩阵，所以你不需要改变它。

示例 3:

输入: mat = [[1,0,0],[1,0,0]]
输出: -1
解释: 该矩阵无法转变成全零矩阵

提示:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 3
• mat[i][j] 是 0 或 1 。

题解 (Rust)

1. 题解

use std::collections::VecDeque;

impl Solution {
    pub fn min_flips(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut min_steps = vec![None; 1 << (m * n)];
        let mut deque = VecDeque::new();
        let mut bin_mat = 0;

        for row in 0..m {
            for col in 0..n {
                bin_mat |= (mat[row][col] as usize) << (row * n + col);
            }
        }

        min_steps[bin_mat] = Some(0);
        deque.push_back(bin_mat);

        while let Some(x) = deque.pop_front() {
            if x == 0 {
                break;
            }

            for row in 0..m {
                for col in 0..n {
                    let mut y = x;

                    y ^= 1 << (row * n + col);
                    y ^= ((row > 0) as usize) << (row * n + col - n);
                    y ^= ((row < m - 1) as usize) << (row * n + col + n);
                    y ^= ((col > 0) as usize) << (row * n + col - 1);
                    y ^= ((col < n - 1) as usize) << (row * n + col + 1);

                    if min_steps[y].is_none() {
                        min_steps[y] = Some(min_steps[x].unwrap() + 1);
                        deque.push_back(y);
                    }
                }
            }
        }

        min_steps[0].unwrap_or(-1)
    }
}