README_CN.md

1091. 二进制矩阵中的最短路径

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

• 路径途经的所有单元格都的值都是 0 。
• 路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。

畅通路径的长度 是该路径途经的单元格总数。

示例 1:

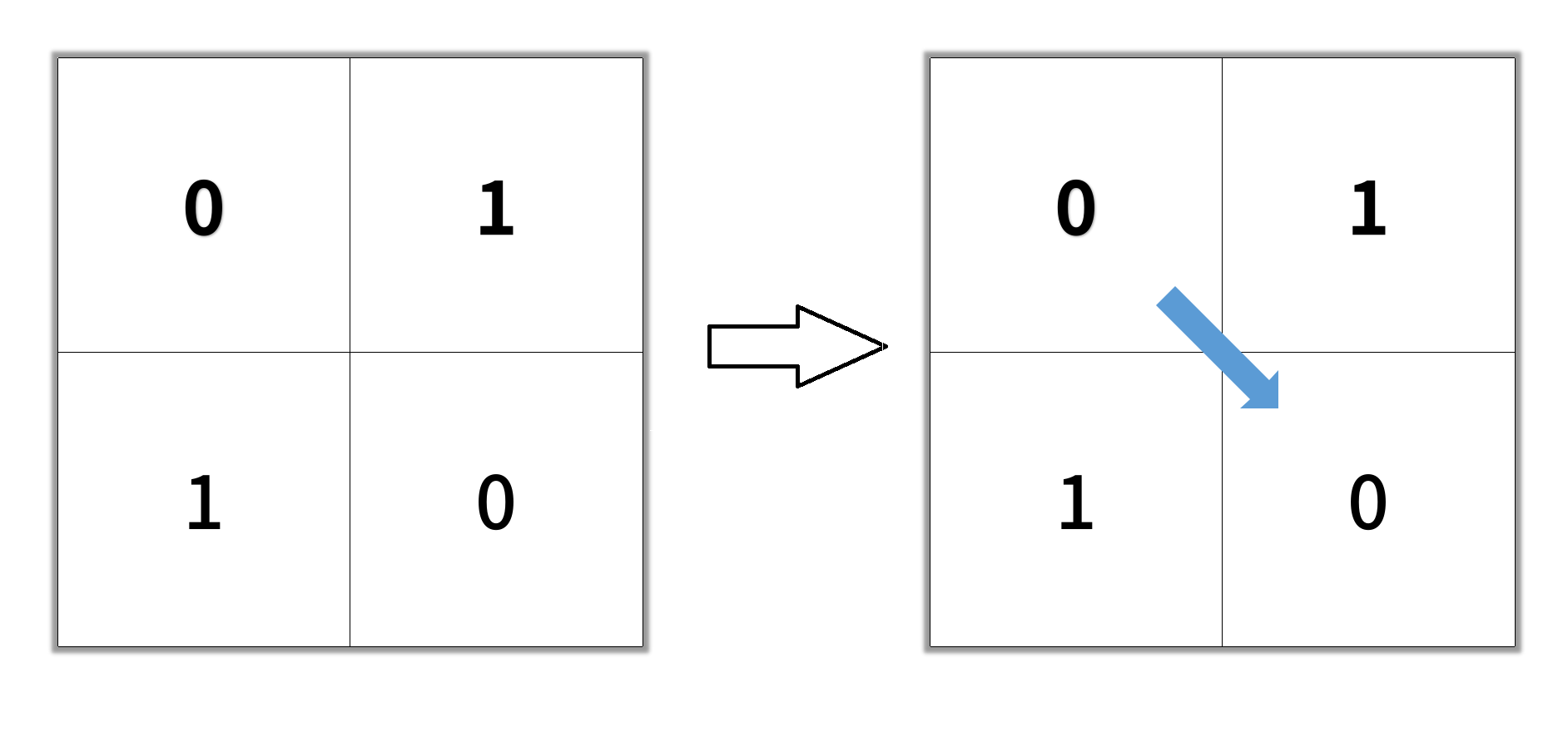
输入: grid = [[0,1],[1,0]]
输出: 2

示例 2:

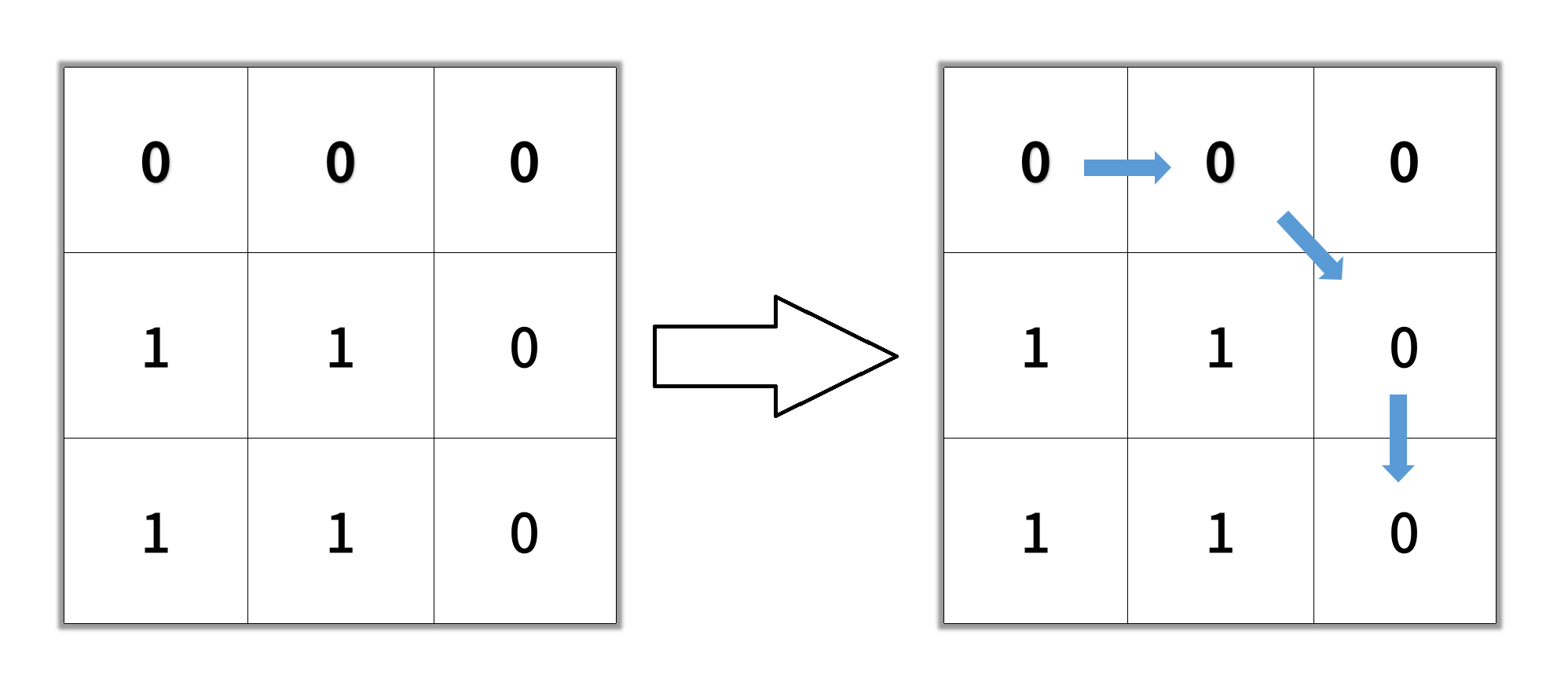
输入: grid = [[0,0,0],[1,1,0],[1,1,0]]
输出: 4

示例 3:

输入: grid = [[1,0,0],[1,1,0],[1,1,0]]
输出: -1

提示:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] 为 0 或 1

题解 (Rust)

1. 广度优先搜索

use std::collections::HashSet;
use std::collections::VecDeque;

impl Solution {
    pub fn shortest_path_binary_matrix(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut seen = vec![(0, 0)].into_iter().collect::<HashSet<_>>();
        let mut cells = vec![(0, 0, 1)].into_iter().collect::<VecDeque<_>>();

        if grid[0][0] == 1 || grid[n - 1][n - 1] == 1 {
            return -1;
        }

        while let Some((x, y, length)) = cells.pop_front() {
            if x == n - 1 && y == n - 1 {
                return length;
            }
            for x_ in x.saturating_sub(1)..(x + 2).min(n) {
                for y_ in y.saturating_sub(1)..(y + 2).min(n) {
                    if grid[x_][y_] == 0 && !seen.contains(&(x_, y_)) {
                        seen.insert((x_, y_));
                        cells.push_back((x_, y_, length + 1));
                    }
                }
            }
        }

        -1
    }
}