README_CN.md

994. 腐烂的橘子

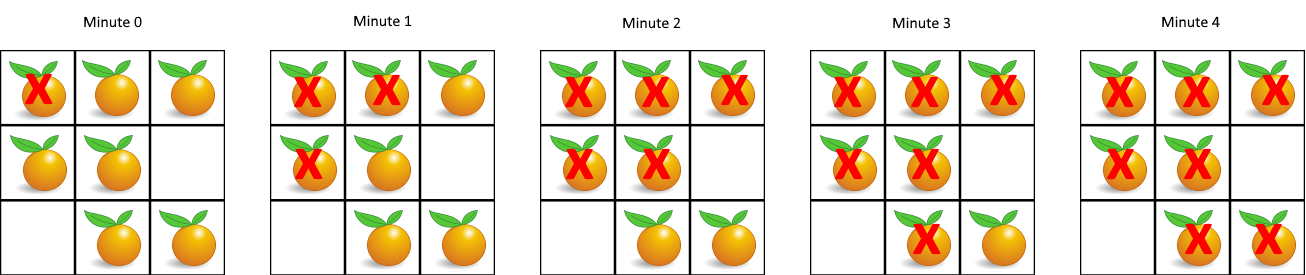
在给定的网格中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例 1:

输入: [[2,1,1],[1,1,0],[0,1,1]]
输出: 4

示例 2:

输入: [[2,1,1],[0,1,1],[1,0,1]]
输出: -1
解释: 左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3:

输入: [[0,2]]
输出: 0
解释: 因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示:

1. 1 <= grid.length <= 10
2. 1 <= grid[0].length <= 10
3. grid[i][j] 仅为 0、1 或 2

题解 (Rust)

1. 模拟

impl Solution {
    pub fn oranges_rotting(grid: Vec<Vec<i32>>) -> i32 {
        let mut prev = grid;

        for minute in 0..59 {
            let mut no_fresh = true;
            let mut new = prev.clone();

            for j in 0..prev.len() {
                for k in 0..prev[0].len() {
                    match prev[j][k] {
                        1 => no_fresh = false,
                        2 => {
                            if j > 0 && prev[j - 1][k] == 1 {
                                new[j - 1][k] = 2;
                            }
                            if k > 0 && prev[j][k - 1] == 1 {
                                new[j][k - 1] = 2;
                            }
                            if j < prev.len() - 1 && prev[j + 1][k] == 1 {
                                new[j + 1][k] = 2;
                            }
                            if k < prev[0].len() - 1 && prev[j][k + 1] == 1 {
                                new[j][k + 1] = 2;
                            }
                        },
                        _ => (),
                    };
                }
            }

            if no_fresh {
                return minute;
            }

            prev = new;
        }

        -1
    }
}