README_CN.md

951. 翻转等价二叉树

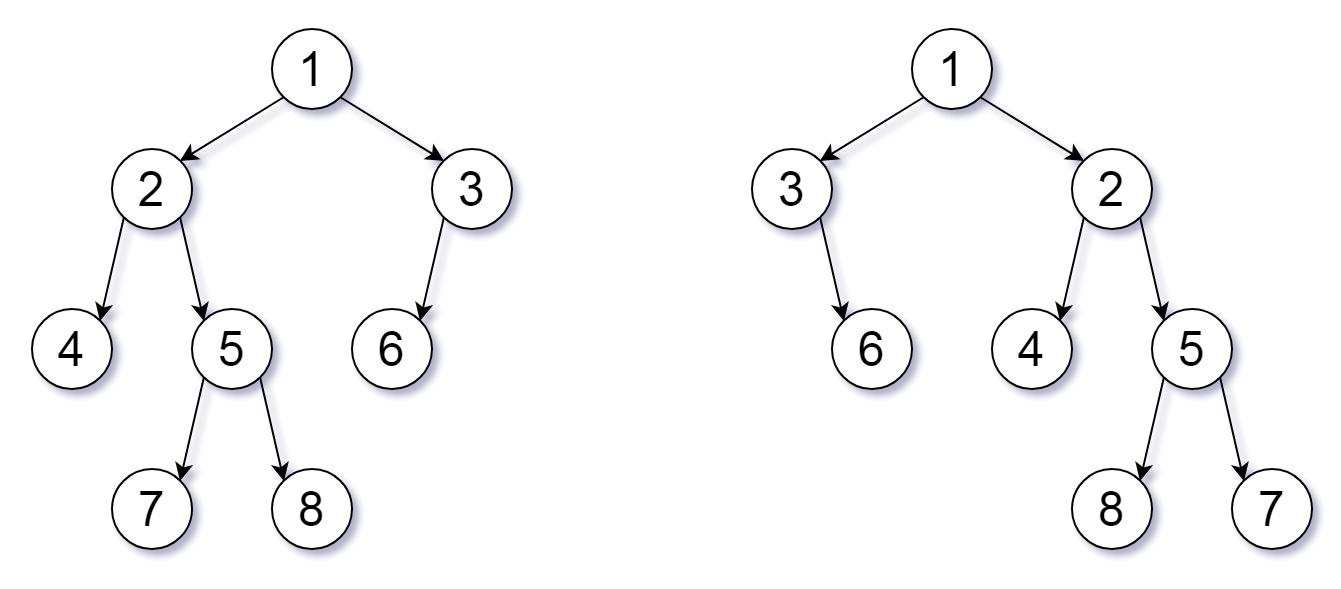
我们可以为二叉树 T 定义一个翻转操作，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y，我们就称二叉树 X 翻转等价于二叉树 Y。

编写一个判断两个二叉树是否是翻转等价的函数。这些树由根节点 root1 和 root2 给出。

示例:

输入: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
输出: true
解释: 我们翻转值为 1，3 以及 5 的三个节点。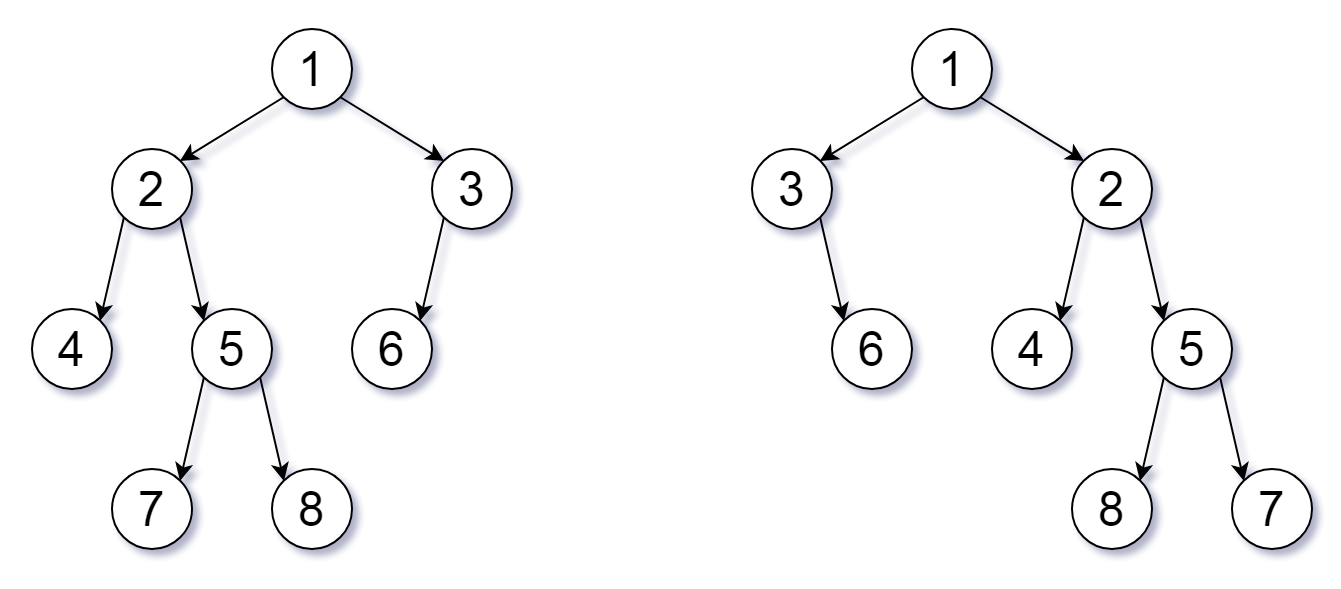

提示:

1. 每棵树最多有 100 个节点。
2. 每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数。

题解 (Ruby)

1. 递归

# Definition for a binary tree node.
# class TreeNode
#     attr_accessor :val, :left, :right
#     def initialize(val = 0, left = nil, right = nil)
#         @val = val
#         @left = left
#         @right = right
#     end
# end
# @param {TreeNode} root1
# @param {TreeNode} root2
# @return {Boolean}
def flip_equiv(root1, root2)
    return true if root1.nil? and root2.nil?
    return false if root1.nil? or root2.nil? or root1.val != root2.val
    return true if flip_equiv(root1.left, root2.left) and flip_equiv(root1.right, root2.right)
    return true if flip_equiv(root1.left, root2.right) and flip_equiv(root1.right, root2.left)
    return false
end