261

261. Graph Valid Tree (Medium)

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

 

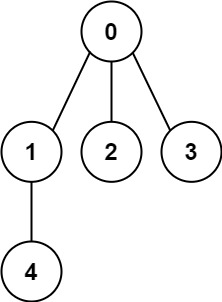
Example 1:

Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

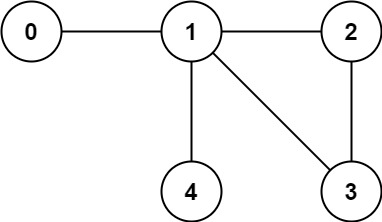
Example 2:

Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

 

Constraints:

• 1 <= n <= 2000
• 0 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no self-loops or repeated edges.

Companies: Google, Bloomberg, TikTok

Related Topics:
Depth-First Search, Breadth-First Search, Union Find, Graph

Similar Questions:

• Course Schedule (Medium)
• Number of Connected Components in an Undirected Graph (Medium)
• Keys and Rooms (Medium)

Solution 1. Union Find

• No cycle
• Single graph component

// OJ: https://leetcode.com/problems/graph-valid-tree/
// Author: github.com/lzl124631x
// Time: O(N + E)
// Space: O(N)
class UnionFind {
    vector<int> id;
    int cnt;
public:
    UnionFind(int N) : id(N), cnt(N) {
        iota(begin(id), end(id), 0);
    }
    int find(int x) {
        return id[x] == x ? x : (id[x] = find(id[x]));
    }
    void connect(int a, int b) {
        id[find(a)] = find(b);
        --cnt;
    }
    bool connected(int a, int b) {
        return find(a) == find(b);
    }
    int getCount() { return cnt; }
};
class Solution {
public:
    bool validTree(int n, vector<vector<int>>& E) {
        UnionFind uf(n);
        for (auto &e : E) {
            if (uf.connected(e[0], e[1])) return false;
            uf.connect(e[0], e[1]);
        }
        return uf.getCount() == 1;
    }
};

Solution 2. DFS

// OJ: https://leetcode.com/problems/graph-valid-tree/
// Author: github.com/lzl124631x
// Time: O(N + E)
// Space: O(N + E)
class Solution {
public:
    bool validTree(int n, vector<vector<int>>& E) {
        if (E.size() != n - 1) return false;
        vector<vector<int>> G(n);
        for (auto &e : E) {
            int u = e[0], v = e[1];
            G[u].push_back(v);
            G[v].push_back(u);
        }
        vector<int> state(n, -1); // -1 unvisited, 0 visiting, 1 visited
        function<bool(int, int)> dfs = [&](int u, int prev) { // returns true if there is no cycle starting from this node u.
            if (state[u] != -1) return state[u] == 1;
            state[u] = 0;
            for (int v : G[u]) {
                if (v == prev) continue;
                if (!dfs(v, u)) return false;
            }
            state[u] = 1;
            return true;
        };
        for (int i = 0; i < n; ++i) {
            if (!dfs(i, -1)) return false;
        }
        return true;
    }
};

Solution 3. BFS

Starting from a random node, 0 for example:

• Can visit n nodes
• No cycle

// OJ: https://leetcode.com/problems/graph-valid-tree/
// Author: github.com/lzl124631x
// Time: O(N + E)
// Space: O(N + E)
class Solution {
public:
    bool validTree(int n, vector<vector<int>>& E) {
        vector<vector<int>> G(n);
        for (auto &e : E) {
            G[e[0]].push_back(e[1]);
            G[e[1]].push_back(e[0]);
        }
        vector<int> depth(n); // depth starts from 1. Depth 0 means unvisited
        int level = 1, total = 0;
        queue<int> q{{0}};
        while (q.size()) {
            int cnt = q.size();
            total += cnt;
            while (cnt--) {
                int u = q.front();
                q.pop();
                depth[u] = level;
                for (int v : G[u]) {
                    if (depth[v] == depth[u]) return false;
                    if (depth[v] == 0) q.push(v);
                }
            }
            ++level;
        }
        return total == n;
    }
};

Solution 4. Topological Sort (BFS)

// OJ: https://leetcode.com/problems/graph-valid-tree
// Author: github.com/lzl124631x
// Time: O(N + E)
// Space: O(N + E)
class Solution {
public:
    bool validTree(int n, vector<vector<int>>& E) {
        if (E.size() != n - 1) return false;
        if (n == 1) return true;
        vector<vector<int>> G(n);
        vector<int> degree(n);
        for (auto &e : E) {
            int u = e[0], v = e[1];
            G[u].push_back(v);
            G[v].push_back(u);
            ++degree[u];
            ++degree[v];
        }
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (degree[i] == 1) q.push(i);
        }
        while (q.size()) {
            int u = q.front();
            q.pop();
            --degree[u];
            --n;
            for (int v : G[u]) {
                if (--degree[v] == 1) q.push(v);
            }
        }
        return n == 0;
    }
};