2271

2271. Maximum White Tiles Covered by a Carpet (Medium)

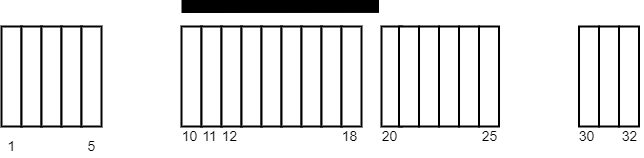
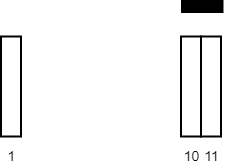
You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.

You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere.

Return the maximum number of white tiles that can be covered by the carpet.

 

Example 1:

Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
Output: 9
Explanation: Place the carpet starting on tile 10. 
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.

Example 2:

Input: tiles = [[10,11],[1,1]], carpetLen = 2
Output: 2
Explanation: Place the carpet starting on tile 10. 
It covers 2 white tiles, so we return 2.

 

Constraints:

• 1 <= tiles.length <= 5 * 104
• tiles[i].length == 2
• 1 <= li <= ri <= 109
• 1 <= carpetLen <= 109
• The tiles are non-overlapping.

Companies: Google

Related Topics:
Array, Binary Search, Greedy, Sorting, Prefix Sum

Similar Questions:

• Maximum Number of Vowels in a Substring of Given Length (Medium)

Solution 1. Two Pointers

// OJ: https://leetcode.com/problems/maximum-white-tiles-covered-by-a-carpet
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(1)
class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& A, int len) {
        sort(begin(A), end(A));
        int N = A.size(), i = 0, j = 0, sum = 0, ans = 0;
        for (; i < N; ++i) {
            int from = A[i][0], to = from + len - 1, part = 0;
            while (j < N && A[j][1] <= to) { // find the fully covered tiles
                sum += A[j][1] - A[j][0] + 1;
                ++j;
            }
            if (j < N && A[j][0] <= to) part = to - A[j][0] + 1;
            ans = max(ans, sum + part);
            if (j > i) sum -= A[i][1] - A[i][0] + 1; // if A[i] is fully covered.
            else ++j;
        }
        return ans;
    }
};