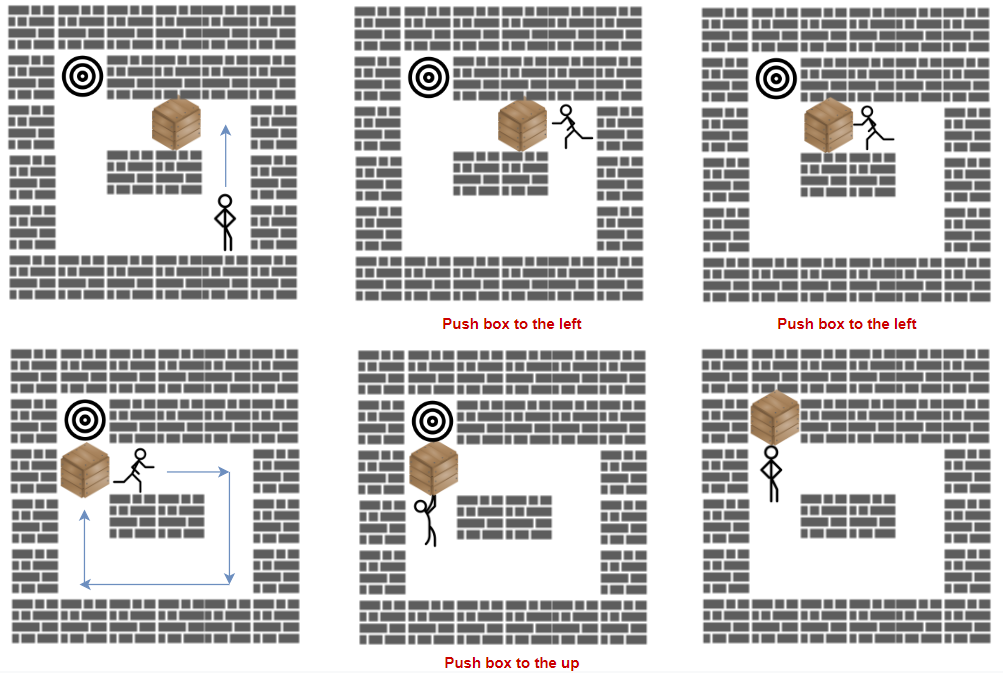
A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.
The game is represented by an m x n grid of characters grid where each element is a wall, floor, or box.
Your task is to move the box 'B' to the target position 'T' under the following rules:
- The character
'S'represents the player. The player can move up, down, left, right ingridif it is a floor (empty cell). - The character
'.'represents the floor which means a free cell to walk. - The character
'#'represents the wall which means an obstacle (impossible to walk there). - There is only one box
'B'and one target cell'T'in thegrid. - The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
- The player cannot walk through the box.
Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.
Example 1:
Input: grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.
Example 2:
Input: grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
Output: -1
Example 3:
Input: grid = [["#","#","#","#","#","#"], ["#","T",".",".","#","#"], ["#",".","#","B",".","#"], ["#",".",".",".",".","#"], ["#",".",".",".","S","#"], ["#","#","#","#","#","#"]] Output: 5 Explanation: push the box down, left, left, up and up.
Example 4:
Input: grid = [["#","#","#","#","#","#","#"], ["#","S","#",".","B","T","#"], ["#","#","#","#","#","#","#"]] Output: -1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 20gridcontains only characters'.','#','S','T', or'B'.- There is only one character
'S','B', and'T'in thegrid.
Companies:
Facebook
Related Topics:
Array, Breadth-First Search, Heap (Priority Queue), Matrix
'.' might be on the edges.
Some moves increase the step if it pushes the box while others doesn't increase the step. Since we want to minimize the moves, we need to prioritize the states with less steps, but this will also prioritize meaningless random wandering, which is not wanted.
dp[sx][sy][bx][by] is the minimal number of pushes needed to make S at (sx, sy) and B at (bx, by).
// OJ: https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/
// Author: github.com/lzl124631x
// Time: O((MN)^2)
// Space: O((MN)^2)
class Solution {
public:
int minPushBox(vector<vector<char>>& A) {
int M = A.size(), N = A[0].size(), tx, ty, sx, sy, bx, by, dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}}, dp[20][20][20][20] = {}, ans = INT_MAX;
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (A[i][j] == 'S') sx = i, sy = j;
else if (A[i][j] == 'B') bx = i, by = j;
else if (A[i][j] == 'T') tx = i, ty = j;
}
}
memset(dp, 0x3f, sizeof(dp));
dp[sx][sy][bx][by] = 0;
queue<array<int, 4>> q{{{sx, sy, bx, by}}};
while (q.size()) {
auto [sx, sy, bx, by] = q.front();
q.pop();
int step = dp[sx][sy][bx][by];
if (bx == tx && by == ty) ans = min(ans, step);
for (auto &[dx, dy] : dirs) {
int a = sx + dx, b = sy + dy, bx2 = bx, by2 = by, step2 = step;
if (a < 0 || a >= M || b < 0 || b >= N || A[a][b] == '#') continue;
if (a == bx && b == by) bx2 += dx, by2 += dy, step2++;
if (bx2 < 0 || bx2 >= M || by2 < 0 || by2 >= N || A[bx2][by2] == '#' || step2 >= dp[a][b][bx2][by2]) continue;
dp[a][b][bx2][by2] = step2;
q.push({a, b, bx2, by2});
}
}
return ans == INT_MAX ? -1 : ans;
}
};