124

124. Binary Tree Maximum Path Sum (Hard)

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

 

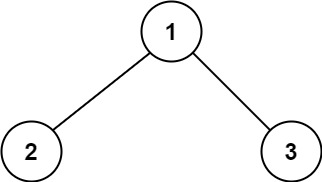
Example 1:

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

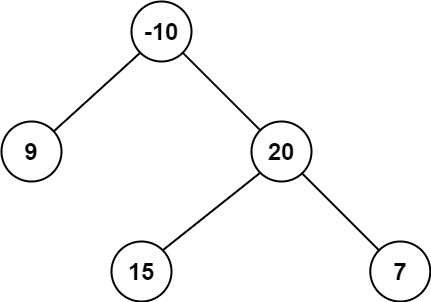
Example 2:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

 

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -1000 <= Node.val <= 1000

Companies:
Facebook, DoorDash, Amazon, Google, Microsoft, Adobe, Samsung, Bloomberg, ByteDance, Myntra, Flipkart

Related Topics:
Dynamic Programming, Tree, Depth-First Search, Binary Tree

Similar Questions:

• Path Sum (Easy)
• Sum Root to Leaf Numbers (Medium)
• Path Sum IV (Medium)
• Longest Univalue Path (Medium)
• Time Needed to Inform All Employees (Medium)

Solution 1. Post-order traversal

For node n, let f(n) be the maximum path sum that STARTS from node n to its children. It means that the path can only go through one of its children, not both of them. We have:

f(n) = n->val + max({ 0, f(n->left), f(n->right) })

For each node n, we also need to try to update the maximum path sum using n->val + max(0, f(n->left)) + max(0, f(n->right)).

In sum, we can use post order traversal to compute f(n) and update maximum path sum along the process.

// OJ: https://leetcode.com/problems/binary-tree-maximum-path-sum/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
    int ans = INT_MIN;
    int dfs(TreeNode *root) {
        if (!root) return 0;
        int left = dfs(root->left), right = dfs(root->right);
        ans = max(ans, root->val + left + right);
        return max(0, root->val + max(left, right));
    }
public:
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return ans;
    }
};