-
Notifications
You must be signed in to change notification settings - Fork 0
/
sm5_differential_expression_analysis.Rmd
786 lines (512 loc) · 39.6 KB
/
sm5_differential_expression_analysis.Rmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
---
title: "STAT 540 - Seminar 5: Differential Expression Analysis"
output: github_document
---
## Attributions
This seminar was developed by Keegan Korthauer from materials previously designed by Eric Chu, Dr. Jenny Bryan, and Alice Zhu.
## Learning Objectives
By the end of this seminar, you should
* have a clear understanding of what differential expression is and how it can be tested
* have practical experience browsing and manipulating real gene expression data
* have practical experience plotting expression changes as a trajectory using ggplot2
* have practical experience testing for differential expression in a single gene using `lm()`
* have practical experience finding differential expressions in a large number of genes and across multiple covariates using `limma()`
* have an intuition of how limma works in the context of "moderated" t-values
* be able to perform genome wide differential expression analysis given expression data and covariates and interpret the resulting statistics
## Packages required
We first load the packages we will use. We have previousy used `knitr`, `tidyverse` and `GEOquery`. Today, we will also use [limma](http://bioconductor.org/packages/release/bioc/html/limma.html).
* If you don't have it already, first install the Bioconductor package manager package: `install.packages("BiocManager")`
* Then install limma with `BiocManager::install("limma")`
```{r load, echo=TRUE, results='hide', message=FALSE, warning=FALSE}
library(knitr)
library(tidyverse)
library(GEOquery)
library(limma)
```
## Functions used
* **`utils::read.table()`** - Reads a file in table format and creates a dataframe from it.
* **`base::c()`** - Combine arguments into a single data structure; for example, c(1,2,3) -> a vector containing 1, 2, and 3.
* **`base::names()`** - Functions to get or set the names of an object (vector, tibble, data frame, etc).
* **`base::factor()`** - The function factor is used to encode a vector as a factor.
* **`base::ncol()`** - Get the number of columns in a dataframe.
* **`base::nrow()`** - Get the number of rows in a dataframe.
* **`base::sort()`** - Sort a vector into ascending or descending order.
* **`tibble::rownames_to_column()`** - Opposite to `column_to_rownames()`; convert row names to a column inside a dataframe.
* **`tibble::column_to_rownames()`** - Opposite to `rownames_to_column()`; convert a column into a dataframe's row names.
* **`tibble::as_tibble()`** - Convert a dataframe to a tibble.
* **`dplyr::pivot_longer()`** - Reduces the number of columns by moving values from all columns to one value per row, lengthening the data dimensions.
* **`base::t()`** - Transpose a matrix or dataframe.
* **`stats::t.test()`** - Performs one and two sample t-tests on vectors of data.
* **`stats::lm()`** - Fit linear models.
* **`base::summary()`** - Generic function used to produce result summaries of the results of various model fitting functions.
* **`stats::aov()`** - Fit an analysis of variance model by a call to lm for each stratum.
* **`knitr::kable()`** - Table generator for R-Markdown.
* **`base::all()`** - Given a set of logical vectors, are all of the values true?
* **`stats::model.matrix()`** - Creates a design (or model) matrix, e.g., by expanding factors to a set of summary variables.
* **`limma::lmFit()`** - Fit linear model for each gene given a series of arrays.
* **`limma::eBayes()`** - Empirical Bayes Statistics for Differential Expression.
* **`limma::topTable()`** - Extract a table of the top-ranked genes from a linear model fit.
* **`limma::makeContrasts()`** - Construct the contrast matrix corresponding to specified contrasts of a set of parameters.
* **`limma::contrast.fit()`** - Given a linear model fit to microarray data, compute estimated coefficients and standard errors for a given set of contrasts.
* **`limma::decideTests()`** - Identify which genes are significantly differentially expressed for each contrast from a fit object containing p-values and test statistics.
* **`base::intersect()`** - Set intersection.
* **`base::as.character()`** - Coerce object to character type, e.g. convert a factor into character.
* **`utils::head()`** - Return first part of a object (a vector or dataframe).
## Part 1: Introduction
### What is differential gene expression, anyway? And why statistics?
If the idea of differential gene expression sounds completely strange, make sure to review the relevant lecture notes and slides before you start. But, just briefly, for our purpose, the expression of a gene is simply the amount of its mRNA molecule that has been detected; the higher the abundance of mRNA detected, the higher the expression. And as with most other scientists, bioinformaticians are also interested in measuring differences between conditions. So, we'd like to know if genes are differentially expressed across 'conditions': e.g. healthy vs. disease, young vs. old, treatment vs. control, heart tissue vs skeletal muscle tissue, etc. And we have an elaborate statistical framework that helps us make this assessment.
Specifically, we may take a single gene and assess whether it is differentially expressed across some conditions. Or we may perform differential expression analysis on a large set of genes (sometimes all ~20,000 genes in the human genome) and do a high throughput screen to detect differentially expressed genes across some conditions. In this seminar, we will work through both scenarios. The approaches are fundamentally the same, but are also quite different, as you will soon see.
First, we introduce the gene expression dataset: its usual format & organization. We will import a sample dataset and render a few plots and tables to get you oriented. Next, we perform differential expression analysis on a single gene. This will be important for understanding the fundamental approach for assessing differential expression. Finally, we perform a genome wide differential expression screen using `limma` (a popular R package).
## Part 2: Gene expression data
So, what does gene expression data look like?
In this seminar, we will use the GSE4051 dataset. See [here](https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE4051) for more details about the dataset. This is the same data set we've been exploring in class!
### Import data
First we import the dataset. Note that we could read in the individual expression data table and meta data table separately, but we'll make use of what we learned in last seminar, and obtain this data directly from GEO using the `GEOquery` package. When fetching a "GSE" accession, the `getGEO` function will return a list of `ExpressionSet` objects (more on that in a bit), so we'll use `[[1]]` notation to grab the first (and only) element of that list.
```{r}
eset <- getGEO("GSE4051", getGPL = FALSE)[[1]]
eset
```
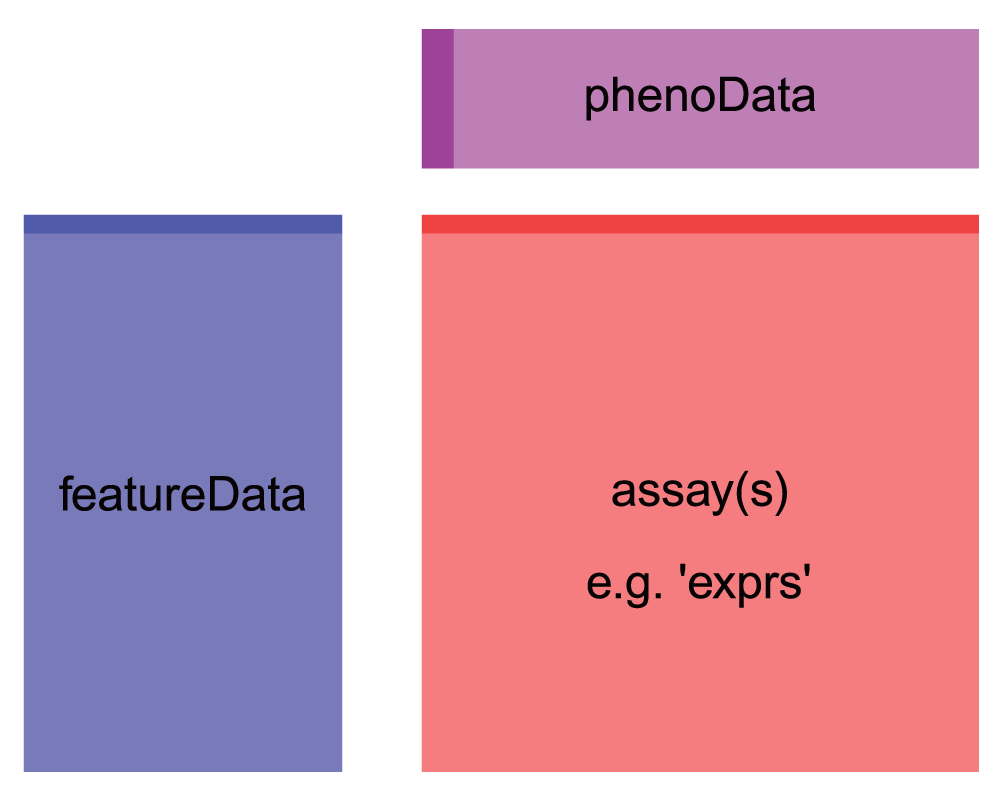
First, we notice that the object we get out is a specially formatted object of class `ExpressionSet`. It has slots for the assay (expression) data (`assayData`), and sample metadata (`phenoData`). We also have some feature (gene) metadata in a slot called `featureData`. Note that this object format is very similar to the `SummarizedExperiment` objects we learned about in class - so this data is organized the Bioconductor way, with all data housed in one object (that we are calling `eset`). Note that we could convert this directly into a `SummarizedExperiment` object by calling `SummarizedExperiment(eset)`. But we'll stick with this format since it will serve our purposes just fine.
Let's take a peek at what's in the **expression matrix**, which we can access from the `ExpressionSet` object with `exprs()`. It contains the sample IDs and their corresponding gene expression profiles. Essentially, each column is a different sample (a tissue, under some treatment, during some developmental stage, etc) and each row is a gene (or a probe). The expression values for all of the genes in a single column collectively constitute the gene expression profile of the sample represented by that column.
Here, we'll print out a small subset (first 5 rows and first 4 columns) of this matrix so you have an idea what it looks like. Note that the gene (probe) names are stored as rownames. The column names (starting with GSM) indicate Sample IDs.
```{r}
exprs(eset)[1:5,1:4]
```
Now let's explore the properties associated with each sample. For example, does sample GSM92610 belong to treatment or control? What developmental stage is it in? What tissue is it? How about sample GSM92611? GSM92612?
Without this information, the expression matrix is pretty much useless, at least for our purpose of assessing differential expression across conditions.
This information is stored in the **samples metadata**. Here we pull that out of the `ExpressionSet` object and take a peek at it using the `pData()` accessor function. We see that we have 36 variables for each of our 39 samples. We'll print the first 3 variables for the first 6 rows.
```{r}
str(pData(eset))
head(pData(eset)[,1:3])
```
Notice that the developmental stage and genotype information are contained in the variable called 'title'. In order to work with these as separate variables, we'll need to do some data wrangling.
```{r}
pData(eset) <- pData(eset) %>%
mutate(sample_id = geo_accession) %>%
mutate(dev_stage = case_when(
grepl("E16", title) ~ "E16",
grepl("P2", title) ~ "P2",
grepl("P6", title) ~ "P6",
grepl("P10", title) ~ "P10",
grepl("4 weeks", title) ~ "4_weeks"
)) %>%
mutate(genotype = case_when(
grepl("Nrl-ko", title) ~ "NrlKO",
grepl("wt", title) ~ "WT"
))
pData(eset) %>%
with(table(dev_stage, genotype))
```
Right now, the `dev_stage` and `genotype` variables are character variables. However, they are more appropriately represented as factors since they have a finite set of categories. You can read more about factors [here](http://r4ds.had.co.nz/factors.html). Basically, factors are categorical variables. By declaring a variable as a factor, many operations on categorical data become easier, such as making separate graphs for each categorical grouping. Generally, it is recommended to use factors where appropriate.
Now, let's turn `dev_stage` and `genotype` into factors. If your categories have a particular order, you can specify them using the "levels" variable in order of increasing value (level1 < level 2 < level3 for levels = c("level1", "level2", "level3")). Here, we'll put the developmental stages in chronological order.
```{r}
pData(eset) <- pData(eset) %>%
mutate(dev_stage = fct_relevel(dev_stage, "E16", "P2", "P6", "P10", "4_weeks")) %>%
mutate(genotype = as.factor(genotype))
# note that Levels contain all possible categories of the variable, and are in the designated order
pData(eset)$dev_stage
pData(eset)$genotype
```
Notice that the samples metadata contains the properties of each sample. So far, we've only printed out a subset of the entire dataset to avoid filling up the entire page. Let's now do a quick sanity check make sure the samples match between the two data frames *exactly*.
```{r}
# number of samples in the expression matrix
ncol(exprs(eset))
# number of samples in the samples metadata
nrow(pData(eset))
# do these numbers match? Let's also print them out
exprs(eset) %>% colnames()
pData(eset)$sample_id
# do the samples match?
identical(exprs(eset) %>% colnames(),
pData(eset)$sample_id)
```
Yes, the samples in both data frames match, and are in exactly the same order! We have metadata for every sample in the expression matrix. Now we're ready to make some plots :).
### What are genes? What are probes?
One last note just before we get the party started. Notice that the row IDs in the expression matrix don't look much like genes. They look like this: 1415670_at, 1415671_at, 1415672_at. What are these random gibberish? Actually these are probe IDs. Probes are segments of sequences used in microarray to bind to segments of cDNA molecules (stretches of mRNA). This means that there may be multiple probes that map to different sections of the same gene and there may be multiple genes that map to the same probe.
For the purpose of our seminar, we will ignore the difference between genes and probes, thereby avoiding the whole mapping problem. Instead, we will simply use these terms interchangeably. When we say "this gene is differentially expressed", feel free to substitute that for "this probe is differentially expressed" and vice versa.
### Plotting gene expression
Ok, now that we've loaded the data, let's do some quick exploration.
Two of the quickest visualizations to screen for problems with the dataset are boxplots and density plots.
Yes, we expect certain genes to be differentially expressed across some conditions. But we do not expect all the genes in a few particular samples to differ from all other samples. If we compare the expression value for all genes from one sample to another, we expect their distributions to line up. This is the rationale for doing such sanity checks.
One of the most common transformations you want to do is convert your data from wide to long format, so it is easily workable by ggplot. This means, convert multiple columns with numeric values to one single column using a given column as pivot, for doing so you can use `pivot_longer()` from `tidyr.` The opposite to `pivot_longer()` is `pivot_wider()`. We recommend that you play around with these functions to get an idea of how they work.
Here we'll pull the data out of the `ExpressionSet` object and into a long tidy table (switching from the "Bioconductor way" to the "Tidy way").
```{r}
# transform into a format ggplot can easily work with
# we add row names (gene names) to a column, then
# we tell pivot_longer to transform all columns but gene
longExpressionMatrix <- exprs(eset) %>%
as.data.frame() %>%
rownames_to_column("gene") %>%
pivot_longer(cols = !gene,
values_to = "Expression",
names_to = "sample_id")
longExpressionMatrix
```
Note we've transformed the 45101 by 39 matrix to a single column with length 1759939. So we have one row for every gene and sample combination.
Actually, let's put this data transformation code from the last two steps into a function so that it can be reused; we will routinely need the dataset to be in this format as we make plots.
```{r}
toLonger <- function(expressionMatrix) {
expressionMatrix <- longExpressionMatrix <- expressionMatrix %>%
as.data.frame() %>%
rownames_to_column("gene") %>%
pivot_longer(cols = !gene,
values_to = "Expression",
names_to = "sample_id")
return(expressionMatrix)
}
```
Note that knowing how to use functions will go a long way in helping you reduce the amount of code you need to write. It also greatly simplifies your code base. Very much recommended!
Okay, now, let's try using this function.
```{r}
toLonger(exprs(eset))
```
Yay! Now we can use the `toLonger` function to pull out the long format expression data.
Next we'll make some distribution plots.
```{r}
toLonger(exprs(eset)) %>%
ggplot(aes(x = sample_id, y = Expression)) +
geom_boxplot() +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
toLonger(exprs(eset)) %>%
ggplot(aes(x = Expression, color = sample_id)) +
geom_density() +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
```
The distribution of gene expression for all genes across all samples look quite consistent. Let's move on!
## Part 3: Single gene analysis
In this section, we will look at differential expression at the single gene level. But first - what does differential expression look like?? More plots!
### What does differential expression look like?
As an example, let's first take a look at gene 1429226_at. We will plot the expression of this gene for every sample, grouped by genotype (wt vs. NrlKO).
```{r}
geneIds <- c("1416119_at", "1431708_a_at")
# use dplyr::filter() to get the expression data for the gene
expressionDataForGene <- toLonger(exprs(eset)) %>%
filter(gene %in% geneIds)
```
Now, we'll integrate the samples metadata by doing a join.
The `left_join()` function ensures that all rows in the first data frame are retained while unmatched rows in the second data frame are dropped. Feel free to run `?join()` in the R-Studio console to learn more as well as other variations of the function such as `right_join()`, `inner_join()`, `full_join()`, etc.
For simplicity, we'll join just the relevant columns of the metadata (`sample_id`, `dev_stage`, and `genotype`) instead of all columns.
```{r}
expressionDataForGene <- expressionDataForGene %>%
left_join(pData(eset) %>% select(sample_id, dev_stage, genotype),
by = "sample_id")
expressionDataForGene
```
Beautiful! Now, what we have is one data frame that contains all the metadata for all samples as well as the gene expression for the genes that we're interested in.
Note that we could also add the join metadata step to our previous function. We'll make the expected input be an `ExpressionSet` object since we'll be accessing both `exprs()` and `pData()` within the function.
```{r}
toLongerMeta <- function(expset) {
stopifnot(class(expset) == "ExpressionSet")
expressionMatrix <- longExpressionMatrix <- exprs(expset) %>%
as.data.frame() %>%
rownames_to_column("gene") %>%
pivot_longer(cols = !gene,
values_to = "Expression",
names_to = "sample_id") %>%
left_join(pData(expset) %>% select(sample_id, dev_stage, genotype),
by = "sample_id")
return(expressionMatrix)
}
toLongerMeta(eset)
```
Finally time for more plots. Not lying, promise.
First, let's look at a couple of genes
```{r}
expressionDataForGene %>%
ggplot(aes(x = Expression, y = genotype, color = genotype)) +
geom_point(size = 3, shape = 1) +
facet_wrap(~gene)
```
Take a moment to look at these plots. Do you think one of these genes is differentially expressed across wt and NrlKO conditions?
If you think that **1431708_a_at** on the right is a hit while **1416119_at** on the left is pretty boring, you'd be right. But why do you think that? Hint: mean and variance.
### The two-group t-test
Of course, eyeballing the data isn't always the best. We need a formal statistical test to tell us how much confidence we should have in the hit, and whether the boring gene is actually boring.
And what's the statistical test is best suited for the scenario where we want to test whether two samples differ in their means? The t-test, of course, it's in the title, not that you needed this bit of help :P.
Let's first do a t-test to compare the expression values across the two genotypes for the boring gene.
```{r}
boringGene <- expressionDataForGene %>% filter(gene == "1416119_at")
t.test(Expression ~ genotype, boringGene)
```
As expected, we obtain a p-value of >0.8. Not so significant. This gene is probably not differentially expressed across the two genotypes, as you suspected based on the plots above.
Now let's run the t-test on the interesting gene.
```{r}
interestingGene <- expressionDataForGene %>% filter(gene == "1431708_a_at")
t.test(Expression ~ genotype, interestingGene)
```
And, we get a p-value < 7.35e-12. An extremely tiny p-value!... Suppose, we set the significance threshold at 0.001, this p-value is statistically significant. We can also see that the mean expression value between the two conditions of this gene ~=2.
### The mighty linear regression
What does the linear regression have to do with this? Turns out, everything. If you're not sure what I'm talking about, make sure to go back to the lectures slides! I would also recommend reading chapter 3 of [An Introduction to Statistical Learning](http://www-bcf.usc.edu/~gareth/ISL/index.html) by Gareth et al. The PDF is freely available [here](http://www-bcf.usc.edu/~gareth/ISL/ISLR%20Seventh%20Printing.pdf).
But essentially, the t-statistics is simply a formulation for testing the relationship between variables based on a linear fit.
To drive the point home, see that we can perform the "t-test" using the linear model in R.
First for the boring gene... We'll use our handy function to grab the nicely formatted long expression table *with metadata added* and filter for the boring gene, then pass to `lm`.
```{r}
boringGene <- toLongerMeta(eset) %>% filter(gene == "1416119_at")
summary(lm(Expression ~ genotype, boringGene))
```
We get a p-value of >0.85, which is what we got with the t-test.
Let's try it with the interesting gene.
```{r}
interestingGene <- toLongerMeta(eset) %>% filter(gene == "1431708_a_at")
summary(lm(Expression ~ genotype, interestingGene))
```
Again, as expected, we get a p-value of ~7.68e-12, similar to the t-test. This is not a coincidence!
By using the linear model instead of the t-test, we free ourselves from making only two-group comparisons. We can now tackle much more complicated situations where there are multiple covariates, each with multiple groups, etc.
As you might realize that to test for differences in multiple groups, we can use ANOVA. Turns that, that's also just a formulation of linear regression.
This is ANOVA. We use it to test if at least one developmental stage is different among all developmental stages (multiple groups) for 1431708_a_at.
```{r}
interestingGene <- toLongerMeta(eset) %>% filter(gene == "1431708_a_at")
summary(aov(Expression ~ dev_stage, interestingGene))
```
We obtain a p-value that is quite big. Let's see what we get with the linear model.
```{r}
interestingGene <- toLongerMeta(eset) %>% filter(gene == "1431708_a_at")
summary(lm(Expression ~ dev_stage, interestingGene))
```
And we get exactly the same p-value for the F-statistic! Again, not a coincidence!
Look like there isn't much differential expression going on for this gene between the developmental stages :D.
## Part 4: Lots of genes (the high-throughput approach)
Part 3 is about assessing whether there is differential expression for a single gene across some conditions. You also saw that we can use the linear model for this task, regardless of how many covariates and groups we have.
So how is assessing one gene any different from assessing 20,000 genes? You ask.
Great question! The intuitive approach is, of course, simply fit a linear model for every gene. Make your comparison between the groups, and then obtain a p-value for each gene. The genes with the p-values that pass the significant threshold are then hits!
Sounds like a great approach! Except there are two problems. First, gene expression data is usually very high dimensional. This means a lot of variables are measured using very few samples. This leads to some biased estimates of variance, leading to bad estimates of p-values. Second, there is the multiple testing problem. It helps to think about what the p-value actually means: the probability of obtaining the test-statistics you obtained by chance. So what's the probability of obtaining a p-value of 0.05 by chance? %5 of course. And this is a problem when you're doing a separate t-test for all 20,000 genes!
We address each of these problems in more detail below.
### Bad variance estimates
Here we provide a data simulation to illustrate why gene variance estimates are bad in gene expression data. We simulate data for 3 samples, each with expression for 1000 genes. We then calculate the variance for each gene give the three samples. Finally, we look at the distribution of these variance estimates.
```{r}
set.seed(124)
numberOfGenes <- 1000
numberOfSamples <- 3
# each row is a gene, each column is a sample
simulatedGeneExpressionMatrix <- matrix(rnorm(numberOfGenes * numberOfSamples), nrow = numberOfGenes)
simulatedGeneExpressionMatrix %>% head()
geneVars <- simulatedGeneExpressionMatrix %>% apply(1, var) # work out the variance for each gene
tibble(variance = geneVars) %>%
ggplot(aes(x = variance)) +
geom_density() +
geom_point(aes(y = 0), shape = 1, size = 3)
```
Notice how many of the observed variances are freakishly small (and freakishly large!), even though they are indeed equal to 1 “on average”. For example, we see that at least a quarter of the genes appear to exhibit a sample variance that is less than one-third the true variance. This can wreak havoc with statistical inference, such as t-statistics. This is what limma – or the statistical methods it embodies, actually – is designed to combat.
Basically, low variance leads to high t-statistics, which in turn leads to low p-values. This means we can end up with a lot of false-positives if we mindlessly use the statistical tools for this kind of high dimensional data.
limma fixes this by using moderated t-values where the "typical variance" is used to weight gene-specific variance estimates. Otherwise, limma is the same as plain old linear regression method.
### Multiple testing: what are the chances of obtaining statistical significance value by random chance?
Multiple testing is another problem that we need to account for. Think about what the p-value actually measures. By definition, the p-value is the **probability of making the observation you made by chance**. Therefore, the p-value of 0.05 suggests that you would get the observation simply by chance 0.05 of the time. Interestingly, 0.05 of 20,000 genes is 1000 genes! If statistical significance was taken at face value, then you would end up with 1000 differentially expressed genes, when none really exist.
Here is an XKCD joke on multiple hypothesis testing [image_MHT](https://imgs.xkcd.com/comics/significant.png)
The capability to handle multiple testing is also built directly into limma. By using the function topTable(), we can make multiple testing adjustments to the significance measures. Limma also provides multiple methods for doing these adjustments. Make sure to go back to the lecture slides if you're feeling fuzzy the concept of multiple testing.
### Limma in action
Now we demonstrate how to use limma for performing large-scale differential expression analysis .
Here, we look for genes differentially expressed across different developmental stages. We first constrain our search to the wild-type samples, excluding any effect that the alternative genotype may have. Using this as an example, we showcase the overall workflow of limma and its various features. Subsequently, we include the alternative genotype samples to show interaction effects.
As usual, to get the most out of this seminar, you should reproduce the step-by-step procedure on your own machine! And note that there are many different ways to perform each step.
```{r}
# get tidy (long) table containing expression + metadata of wild type samples (useful for plotting later on)
wildType_long <- toLongerMeta(eset) %>%
filter(genotype == "WT")
# pull out just metadata for wildtype samples
wildTypeMetadata <- pData(eset) %>%
filter(genotype == "WT") %>%
select(sample_id, genotype, dev_stage)
# pull out just expression data for wildtype samples
# makes use of the fact that the eset has column (sample) names
wildTypeExpressionMatrix <- exprs(eset[, wildTypeMetadata$sample_id])
```
Now we have filtered for only wild-type samples in both the samples metadata and the expression matrix.
Next we want to construct the design matrix. The design matrix dictates how the categorical covariates are parameterized in the linear model. If you're not sure what this means, make sure to get help. This is an important concept! We also recommend reading chapter 3 of [An Introduction to Statistical Learning](http://www-bcf.usc.edu/~gareth/ISL/index.html) by Gareth et al.
Before we actually construct the design matrix, there is one thing we need to check. That is, the samples are ordered identically in the samples metadata data frame as well as the expression matrix. The design matrix is constructed based on the order of the samples metadata data frame and is used to conduct differential expression analysis on the expression matrix. This consistency is absolutely critical. As soon as the two data frame go out of sync, the comparisons is no longer accurate.
```{r}
# Ordering of samples in the samples metadata
wildTypeMetadata$sample_id
# Ordering of samples in the expression matrix
colnames(wildTypeExpressionMatrix)
# check equivalence
identical(wildTypeMetadata$sample_id, colnames(wildTypeExpressionMatrix))
```
Very good! Now, we construct the design matrix.
It is recommended that you at least eyeball the design matrix to see if you can spot any problems. We print out the first ten rows of the design matrix and the samples metadata here.
```{r}
designMatrix <- model.matrix(~dev_stage, wildTypeMetadata)
head(designMatrix, 10) %>% kable()
head(wildTypeMetadata, 10) %>% kable()
```
Notice that E16 is taken to be the baseline and everything else is defined relative to it.
Looks good? Let's move on. We now fit the model.
```{r}
# keep the fit around as we will need to it for looking at other contrasts later
wildTypeDevStageFit <- lmFit(wildTypeExpressionMatrix, designMatrix)
# run ebayes to calculate moderated t-statistics
wildTypeDevStageFitEb <- eBayes(wildTypeDevStageFit)
```
Note that `limma` is a Bioconductor package and is actually compatible with storing the data the "Bioconductor way", so we don't need to put the expression data into the tidy long format like we did with `lm`. In fact, we actually don't even need to pull out the expression matrix from the `ExpressionSet` object -- `limma` can do that on its own. Here we check that we get the same results for both types of input.
```{r}
wildTypeDevStageFit_eset <- lmFit(eset[,wildTypeMetadata$sample_id],
designMatrix)
identical(wildTypeDevStageFit, wildTypeDevStageFit_eset)
```
### `topTable()` is your best friend
Now we've fit the models. We can start going through the differentially expressed genes list. We do this using the `topTable()` function.
```{r}
topTenGenes <- topTable(wildTypeDevStageFitEb)
topTenGenes
```
By default, `topTable()` returns the top 10 most statistically significant genes. Let's make a few plots to see how these genes were differentially expressed.
Let's plot the top 6 genes in our list. We will plot the expression of each gene for all the wild-type samples across all the developmental stages.
Remember the `toLongerMeta()` that we wrote? Scroll up if you forgot. We can reuse it here.
```{r}
topGenes <- rownames(topTenGenes)[1:6]
topGenesExpressionData <- toLongerMeta(eset) %>%
filter(genotype == "WT") %>%
filter(gene %in% topGenes)
topGenesExpressionData # reminder of formatted expression data looks like - for easy graphing
topGenesExpressionData %>%
ggplot(aes(x = dev_stage, y = Expression, color = genotype)) +
geom_point(shape = 1, size = 2) +
stat_summary(aes(y = Expression, group=1), fun = mean, geom="line") +
facet_wrap(~gene)
```
What do you think? Does it look plausible to you that these genes are differentially expressed across developmental stages?
Let's look at the least significant genes.
Actually, before we do that, let's put the graphing code into a reusable function that takes two arguments: the list of genes, and the `ExpressionSet` object that contains the expression and metadata:
```{r}
plotGenes <- function(genes, exprset) {
expressionDataForGenes <- toLongerMeta(exprset) %>%
filter(gene %in% genes)
expressionDataForGenes %>%
ggplot(aes(x = dev_stage, y = Expression, color = genotype)) +
geom_point(shape = 1, size = 2) +
stat_summary(aes(y = Expression, group=1), fun = mean, geom="line") +
facet_wrap(~gene)
}
# verify that the function works - note that we have to subset the eset to just wild type samples
# unless we want to plot all samples
plotGenes(topGenes, eset[, eset$genotype == "WT"])
```
OK, now let's use `topTable()` again to find some boring (insignificant) genes.
```{r}
allGenes <- topTable(wildTypeDevStageFitEb, number = Inf) # show all genes in the list, rather than just the top 10
nrow(allGenes) # number of genes
# Let's look at the bottom 6 genes
boringGeneIndices <- seq(from = nrow(allGenes), to = nrow(allGenes) - 5)
boringGenes <- allGenes[boringGeneIndices,]
# print out the boring genes and their p-values
boringGenes
```
Notice that the genes on the bottom of our list have very large p-values. Also look at the differences for each group relative to baseline. They're all quite minor. Let's plot them out and see for ourselves.
```{r}
plotGenes(rownames(boringGenes), eset[, eset$genotype == "WT"])
```
Are you convinced?? I hope so!
Explore more with `topTable()`. Run `?topTable()` in your R-Studio Console. Make sure you're familiar with the options to use alternative multiple testing methods, sort by different metrics, apply p-value cutoffs, etc.
### Constructing and using the contrast matrix
Now, remember that everything was assessed relative to the baseline (E16). What if we're particularly interested in finding the genes that are differentially expressed from developmental stages P6 to P10? Or from P10 to 4_weeks? Or both?
This is where the contrast matrix comes in. Again, review the lecture slides or get help from TAs if you're not sure what contrasts are. Essentially, they help you make comparisons between groups, rather than only with the baseline.
In order to make these comparisons, you first have to construct the appropriate contrast matrix using `makeContrasts()`, then fit the contrast using `contrast.fit()`, apply `ebayes()` to calculate moderated statistics again, and then use `topTable()` to get the results.
Let’s try to distinguish genes that have stable expression at the last three developmental stages (P6, P10, and 4_weeks) from those that do not. If expression doesn’t change from P6 to P10 to 4_weeks, then the effects for all 3 of those developmental stages should be the same. That means that the difference between the P10 and P6 effects is zero and ditto for the difference between 4_weeks effect and P10 (or P6, for that matter). Let’s form these contrasts.
```{r}
# construct the contrast matrix
contrastMatrix <- makeContrasts(
p10vsp6 = dev_stageP10 - dev_stageP6,
fourweeksVsP10 = dev_stage4_weeks - dev_stageP10,
levels = designMatrix
)
contrastMatrix # take a look
# fit the contrast using the original fitted model
contrastFit <- contrasts.fit(wildTypeDevStageFit, contrastMatrix)
# apply eBayes() for moderated statistics
contrastFitEb <- eBayes(contrastFit)
```
Now, you can use `topTable()` again to get the results.
```{r}
contrastGenes <- topTable(contrastFitEb)
contrastGenes
# again plot the top 6 genes
plotGenes(rownames(contrastGenes)[1:6], eset[, eset$genotype == "WT"])
```
So far, so good. These 6 probes show little expression change from P6 to P10 and a strong increase from P10 to 4_weeks. I would like to find some where there’s a change in each case but perhaps in opposite direction. Let’s press on.
Let’s use `decideTests()` to adjust the p-values for both contrasts globally, i.e. all together and then threshold them at a cutoff of 1e-04.
```{r}
cutoff <- 1e-04
wtResCont <- decideTests(contrastFitEb, p.value = cutoff, method = "global")
summary(wtResCont)
```
We see there are 4 probes that go down from P6 to P10 and no hits going the other way. There are 8 probes that go down from P10 to 4_weeks and 67 going the other way. Let’s try to pull out various hits and plot their data.
Here are the 4 that decline from P6 to P10.
```{r}
hits1 <- wtResCont %>%
as.data.frame() %>%
rownames_to_column("gene") %>%
filter(p10vsp6 < 0)
# these are the genes that declined from P6 to P10
hits1
# lets plot them
plotGenes(hits1$gene, eset[, eset$genotype == "WT"])
```
Here are 4 of the 8 that decline from P10 to 4_weeks.
```{r}
hits2 <- wtResCont %>%
as.data.frame() %>%
rownames_to_column("gene") %>%
filter(fourweeksVsP10 < 0)
# these are the genes that declined from P10 to 4_weeks
hits2
# lets plot them
plotGenes(hits2$gene[1:4], eset[, eset$genotype == "WT"])
```
Is there any overlap between these probes?
```{r}
hits1$gene %>% intersect(hits2$gene)
```
Doesn't seem so. If there is enough time, repeat this analysis with a less stringent p-value. See if you can get any overlaps. You get the idea. We've demonstrated how to use contrasts to compare between different groups. We've also demonstrated the `decideTests()` function to find significant genes for each contrast.
### Assessing interaction
So far, we've only done analysis on the wild-type samples and pretended that the alternative genotype doesn't exist. What if the genotype information at least partially determines (I don't mean to imply causality here) the effect of developmental stages. In that, the effect of developmental stages is different for the two genotypes.
This is called interaction. And to assess this phenomenon, we must analyze all samples together.
```{r}
# for simplification, let's look at only a two-by-two design, we'll filter for developmental stages E16 and 4_weeks
interactionSamples <- pData(eset) %>%
filter(dev_stage %in% c("E16", "4_weeks")) %>%
select(sample_id, dev_stage, genotype)
# IMPORTANT - you want to adjust factor levels here to eliminate stages P2, P6, and P10 from your design matrix
interactionSamples$dev_stage <- interactionSamples$dev_stage %>%
as.character() %>%
factor(levels = c("E16", "4_weeks"))
# reminder of what samples metadata look like - all samples
interactionSamples
# construct the design matrix to include all groups for genotype and developmental stages plus the interaction terms
interactionDesign <- model.matrix(~genotype*dev_stage, interactionSamples)
interactionDesign
```
Now you have a design that allows you to compare the effect development stage for the two genotypes. The baseline is NrlKO at the E16 developmental stage.
If genotype and developmental stage are interactive, then we should see some genes which are significantly up-regulated over development for one genotype but not the other (perhaps not changed at all, or down regulated). Specifically, these genes would have a differential expression of in the dev_stage4_weeks term in one direction and differential expression in the `genotypeWT:dev_stage4_weeks` term in the opposite direction.
Let's try and find these genes!
```{r}
# first fit the model
interactionFit <- lmFit(eset[, interactionSamples$sample_id],
interactionDesign) %>% eBayes()
# make DE calls for each coefficient
de_calls <- decideTests(interactionFit, method = "global", cutoff = 1e-6) %>%
as.data.frame() %>%
rownames_to_column("gene") %>%
as_tibble()
# look for all genes with significant negative interaction effect and up regulation across developmental stages in KO (simple effect)
which.flip <- de_calls %>%
filter(dev_stage4_weeks > 0, `genotypeWT:dev_stage4_weeks` < 0) %>%
pull(gene)
# sort results by strength of interaction effect; pull out the genes with opposite
# developmental stage simple effect and interaction effect identified above
hits <- topTable(interactionFit, number = Inf,
coef = "genotypeWT:dev_stage4_weeks") %>%
rownames_to_column("gene") %>%
filter(gene %in% which.flip)
# lets try plotting 4 on this list
expressionDataForHits <- toLongerMeta(eset[, eset$sample_id %in% interactionSamples$sample_id]) %>%
filter(gene %in% hits$gene[1:4])
expressionDataForHits %>%
ggplot(aes(x = dev_stage, y = Expression, color = genotype)) +
geom_point(shape = 1, size = 2) +
stat_summary(aes(y = Expression, group = genotype), fun = mean, geom = "line") +
facet_wrap(~ gene)
```
## Part 5: Deliverables
For full marks on this seminar deliverable, construct a plot to visualize the gene expression by developmental stage (E16 and 4W only) for 4 genes that have no significant interaction between genotype and developmental stages. Add trend lines and colour by genotype.
Hint: Start with the code in the previous code chunk, and modify to produce a similar plot but for 4 genes with no significant interaction.
```{r}
# YOUR CODE HERE
```