|
| 1 | +# 2147. Number of Ways to Divide a Long Corridor |
| 2 | + |
| 3 | +- Difficulty: Hard. |
| 4 | +- Related Topics: Math, String, Dynamic Programming. |
| 5 | +- Similar Questions: Decode Ways II, Minimum Cost to Cut a Stick, Ways to Split Array Into Three Subarrays. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +Along a long library corridor, there is a line of seats and decorative plants. You are given a **0-indexed** string `corridor` of length `n` consisting of letters `'S'` and `'P'` where each `'S'` represents a seat and each `'P'` represents a plant. |
| 10 | + |
| 11 | +One room divider has **already** been installed to the left of index `0`, and **another** to the right of index `n - 1`. Additional room dividers can be installed. For each position between indices `i - 1` and `i` (`1 <= i <= n - 1`), at most one divider can be installed. |
| 12 | + |
| 13 | +Divide the corridor into non-overlapping sections, where each section has **exactly two seats** with any number of plants. There may be multiple ways to perform the division. Two ways are **different** if there is a position with a room divider installed in the first way but not in the second way. |
| 14 | + |
| 15 | +Return **the number of ways to divide the corridor**. Since the answer may be very large, return it **modulo** `109 + 7`. If there is no way, return `0`. |
| 16 | + |
| 17 | + |
| 18 | +Example 1: |
| 19 | + |
| 20 | +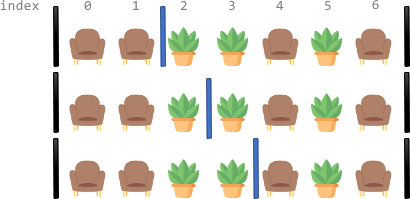 |
| 21 | + |
| 22 | +``` |
| 23 | +Input: corridor = "SSPPSPS" |
| 24 | +Output: 3 |
| 25 | +Explanation: There are 3 different ways to divide the corridor. |
| 26 | +The black bars in the above image indicate the two room dividers already installed. |
| 27 | +Note that in each of the ways, each section has exactly two seats. |
| 28 | +``` |
| 29 | + |
| 30 | +Example 2: |
| 31 | + |
| 32 | + |
| 33 | + |
| 34 | +``` |
| 35 | +Input: corridor = "PPSPSP" |
| 36 | +Output: 1 |
| 37 | +Explanation: There is only 1 way to divide the corridor, by not installing any additional dividers. |
| 38 | +Installing any would create some section that does not have exactly two seats. |
| 39 | +``` |
| 40 | + |
| 41 | +Example 3: |
| 42 | + |
| 43 | +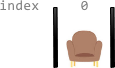 |
| 44 | + |
| 45 | +``` |
| 46 | +Input: corridor = "S" |
| 47 | +Output: 0 |
| 48 | +Explanation: There is no way to divide the corridor because there will always be a section that does not have exactly two seats. |
| 49 | +``` |
| 50 | + |
| 51 | + |
| 52 | +**Constraints:** |
| 53 | + |
| 54 | + |
| 55 | + |
| 56 | +- `n == corridor.length` |
| 57 | + |
| 58 | +- `1 <= n <= 105` |
| 59 | + |
| 60 | +- `corridor[i]` is either `'S'` or `'P'`. |
| 61 | + |
| 62 | + |
| 63 | + |
| 64 | +## Solution |
| 65 | + |
| 66 | +```javascript |
| 67 | +/** |
| 68 | + * @param {string} corridor |
| 69 | + * @return {number} |
| 70 | + */ |
| 71 | +var numberOfWays = function(corridor) { |
| 72 | + var num = BigInt(1); |
| 73 | + var mod = BigInt(Math.pow(10, 9) + 7); |
| 74 | + var seatNum = 0; |
| 75 | + var plantNum = 0; |
| 76 | + for (var i = 0; i < corridor.length; i++) { |
| 77 | + if (corridor[i] === 'S') { |
| 78 | + if (seatNum === 2) { |
| 79 | + num *= BigInt(plantNum + 1); |
| 80 | + num %= mod; |
| 81 | + seatNum = 1; |
| 82 | + plantNum = 0; |
| 83 | + } else { |
| 84 | + seatNum += 1; |
| 85 | + } |
| 86 | + } else { |
| 87 | + if (seatNum === 2) { |
| 88 | + plantNum += 1; |
| 89 | + } |
| 90 | + } |
| 91 | + } |
| 92 | + return seatNum === 2 ? Number(num) : 0; |
| 93 | +}; |
| 94 | +``` |
| 95 | + |
| 96 | +**Explain:** |
| 97 | + |
| 98 | +nope. |
| 99 | + |
| 100 | +**Complexity:** |
| 101 | + |
| 102 | +* Time complexity : O(n). |
| 103 | +* Space complexity : O(1). |
0 commit comments