Skip to content

Commit cae3cd2

Browse files
2xiao2xiao
committed
add 2684
1 parent d472c68 commit cae3cd2

File tree

8 files changed

+341
-7
lines changed

8 files changed

+341
-7
lines changed

‎src/.vuepress/sidebar.ts‎

Lines changed: 1 addition & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -567,6 +567,7 @@ export default sidebar({
567567
"2675",
568568
"2676",
569569
"2677",
570+
"2684",
570571
"2694",
571572
"2695",
572573
"2696"

‎src/plan/contest_list.md‎

Lines changed: 1 addition & 1 deletion
Original file line numberDiff line numberDiff line change
@@ -1357,7 +1357,7 @@ headerDepth: 0
13571357
| :------: | :------ | :------: | :------ | :------ |
13581358
| 2682 | [找出转圈游戏输家](https://leetcode.com/problems/find-the-losers-of-the-circular-game) | | [`数组`](/tag/array.md) [`哈希表`](/tag/hash-table.md) [`模拟`](/tag/simulation.md) | <font color=#15bd66>Easy</font> |
13591359
| 2683 | [相邻值的按位异或](https://leetcode.com/problems/neighboring-bitwise-xor) | | [`位运算`](/tag/bit-manipulation.md) [`数组`](/tag/array.md) | <font color=#ffb800>Medium</font> |
1360-
| 2684 | [矩阵中移动的最大次数](https://leetcode.com/problems/maximum-number-of-moves-in-a-grid) | | [`数组`](/tag/array.md) [`动态规划`](/tag/dynamic-programming.md) [`矩阵`](/tag/matrix.md) | <font color=#ffb800>Medium</font> |
1360+
| 2684 | [矩阵中移动的最大次数](https://leetcode.com/problems/maximum-number-of-moves-in-a-grid) | [[✓]](/problem/2684.md) | [`数组`](/tag/array.md) [`动态规划`](/tag/dynamic-programming.md) [`矩阵`](/tag/matrix.md) | <font color=#ffb800>Medium</font> |
13611361
| 2685 | [统计完全连通分量的数量](https://leetcode.com/problems/count-the-number-of-complete-components) | | [`深度优先搜索`](/tag/depth-first-search.md) [`广度优先搜索`](/tag/breadth-first-search.md) [`图`](/tag/graph.md) | <font color=#ffb800>Medium</font> |
13621362

13631363

‎src/problem/2632.md‎

Lines changed: 103 additions & 2 deletions
Original file line numberDiff line numberDiff line change
@@ -4,11 +4,112 @@
44

55
## 题目
66

7+
Given a function `fn`, return a **curried** version of that function.
8+
9+
A **curried** function is a function that accepts fewer or an equal number of parameters as the original function and returns either another **curried** function or the same value the original function would have returned.
10+
11+
In practical terms, if you called the original function like `sum(1,2,3)`, you would call the **curried** version like `csum(1)(2)(3)`, `csum(1)(2,3) `, `csum(1,2)(3)`, or `csum(1,2,3)`. All these methods of calling the **curried** function should return the same value as the original.
12+
13+
**Example 1:**
14+
15+
> Input:
16+
>
17+
> `fn = function sum(a, b, c) { return a + b + c; }`
18+
>
19+
> `inputs = [[1],[2],[3]]`
20+
>
21+
> Output: 6
22+
>
23+
> Explanation:
24+
>
25+
> The code being executed is:
26+
>
27+
> `const curriedSum = curry(fn);`
28+
>
29+
> `curriedSum(1)(2)(3) === 6;`
30+
>
31+
> `curriedSum(1)(2)(3)` should return the same value as `sum(1, 2, 3)`.
32+
33+
**Example 2:**
34+
35+
> Input:
36+
>
37+
> `fn = function sum(a, b, c) { return a + b + c; }`
38+
>
39+
> `inputs = [[1,2],[3]]`
40+
>
41+
> Output: 6
42+
>
43+
> Explanation:
44+
>
45+
> `curriedSum(1, 2)(3)` should return the same value as `sum(1, 2, 3)`.
46+
47+
**Example 3:**
48+
49+
> Input:
50+
>
51+
> `fn = function sum(a, b, c) { return a + b + c; }`
52+
>
53+
> `inputs = [[],[],[1,2,3]]`
54+
>
55+
> Output: 6
56+
>
57+
> Explanation:
58+
>
59+
> You should be able to pass the parameters in any way, including all at once or none at all.
60+
>
61+
> `curriedSum()()(1, 2, 3)` should return the same value as `sum(1, 2, 3)`.
62+
63+
**Example 4:**
64+
65+
> Input:
66+
>
67+
> `fn = function life() { return 42; }`
68+
>
69+
> `inputs = [[]]`
70+
>
71+
> Output: 42
72+
>
73+
> Explanation:
74+
>
75+
> currying a function that accepts zero parameters should effectively do nothing.
76+
>
77+
> `curriedLife() === 42`
78+
79+
**Constraints:**
80+
81+
- `1 <= inputs.length <= 1000`
82+
- `0 <= inputs[i][j] <= 10^5`
83+
- `0 <= fn.length <= 1000`
84+
- `inputs.flat().length == fn.length`
85+
- function parameters explicitly defined
86+
- If `fn.length > 0` then the last array in `inputs` is not empty
87+
- If `fn.length === 0` then `inputs.length === 1`
88+
89+
## 题目大意
90+
91+
请你编写一个函数，它接收一个其他的函数，并返回该函数的 **柯里化** 后的形式。
92+
93+
**柯里化** 函数的定义是接受与原函数相同数量或更少数量的参数，并返回另一个 **柯里化** 后的函数或与原函数相同的值。
94+
95+
实际上，当你调用原函数，如 `sum(1,2,3)` 时，它将调用 **柯里化** 函数的某个形式，如 `csum(1)(2)(3)`，
96+
`csum(1)(2,3)`， `csum(1,2)(3)`，或 `csum(1,2,3)` 。所有调用 **柯里化** 函数的方法都应该返回与原始函数相同的值。
97+
98+
**提示：**
99+
100+
- `1 <= inputs.length <= 1000`
101+
- `0 <= inputs[i][j] <= 10^5`
102+
- `0 <= fn.length <= 1000`
103+
- `inputs.flat().length == fn.length`
104+
- `函数参数需要被显式定义`
105+
- 如果 `fn.length > 0` 则最后一个数组 `inputs` 不为空
106+
- 如果 `fn.length === 0` 则 `inputs.length === 1`
107+
7108
## 解题思路
8109

9110
[柯里化（Currying）](https://en.wikipedia.org/wiki/Currying)是一种关于函数的高阶技术，它是指将一个函数从可调用的 `f(a, b, c)` 转换为可调用的 `f(a)(b)(c)`。柯里化不会调用函数，只是对函数进行转换。
10111

11-
#### 柯里化的目的是什么？
112+
### 柯里化的目的是什么？
12113

13114
可以从一个实际中的例子中，了解柯里化的好处。
14115

@@ -54,7 +155,7 @@ debugNow('message'); // [HH:mm] DEBUG message
54155

55156
因此，柯里化让我们能够更容易地获取部分应用函数。就像在日志记录示例中看到的那样，普通函数 `log(date, importance, message)` 在被柯里化之后，当调用它的时候传入一个参数（如 `log(date)`）或两个参数（`log(date, importance)`）时，它会返回部分应用函数。
56157

57-
#### 实现柯里化函数的思路
158+
### 实现柯里化函数的思路：
58159

59160
1. **函数参数处理**：
60161

‎src/problem/2684.md‎

Lines changed: 231 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,231 @@
1+
# [2684. 矩阵中移动的最大次数](https://2xiao.github.io/leetcode-js/problem/2684.html)
2+
3+
🟠 <font color=#ffb800>Medium</font>&emsp; 🔖&ensp; [`数组`](/tag/array.md) [`动态规划`](/tag/dynamic-programming.md) [`矩阵`](/tag/matrix.md)&emsp; 🔗&ensp;[`力扣`](https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid) [`LeetCode`](https://leetcode.com/problems/maximum-number-of-moves-in-a-grid)
4+
5+
## 题目
6+
7+
You are given a **0-indexed** `m x n` matrix `grid` consisting of **positive**
8+
integers.
9+
10+
You can start at **any** cell in the first column of the matrix, and traverse
11+
the grid in the following way:
12+
13+
- From a cell `(row, col)`, you can move to any of the cells: `(row - 1, col + 1)`, `(row, col + 1)` and `(row + 1, col + 1)` such that the value of the cell you move to, should be **strictly** bigger than the value of the current cell.
14+
15+
Return _the **maximum** number of **moves** that you can perform._
16+
17+
**Example 1:**
18+
19+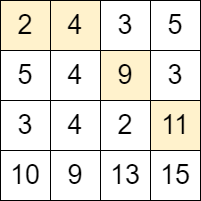
![](https://assets.leetcode.com/uploads/2023/04/11/yetgriddrawio-10.png)
20+
21+
> Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
22+
>
23+
> Output: 3
24+
>
25+
> Explanation: We can start at the cell (0, 0) and make the following moves:
26+
>
27+
> - (0, 0) -> (0, 1).
28+
> - (0, 1) -> (1, 2).
29+
> - (1, 2) -> (2, 3).
30+
>
31+
> It can be shown that it is the maximum number of moves that can be made.
32+
33+
**Example 2:**
34+
35+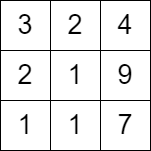
> ![](https://assets.leetcode.com/uploads/2023/04/12/yetgrid4drawio.png)
36+
>
37+
> **Input:** grid = [[3,2,4],[2,1,9],[1,1,7]]
38+
>
39+
> Output: 0
40+
>
41+
> Explanation: Starting from any cell in the first column we cannot perform any moves.
42+
43+
**Constraints:**
44+
45+
- `m == grid.length`
46+
- `n == grid[i].length`
47+
- `2 <= m, n <= 1000`
48+
- `4 <= m * n <= 10^5`
49+
- `1 <= grid[i][j] <= 10^6`
50+
51+
## 题目大意
52+
53+
给你一个下标从 **0** 开始、大小为 `m x n` 的矩阵 `grid` ，矩阵由若干 **正** 整数组成。
54+
55+
你可以从矩阵第一列中的 **任一** 单元格出发，按以下方式遍历 `grid` ：
56+
57+
- 从单元格 `(row, col)` 可以移动到 `(row - 1, col + 1)`、`(row, col + 1)` 和 `(row + 1, col + 1)` 三个单元格中任一满足值 **严格** 大于当前单元格的单元格。
58+
59+
返回你在矩阵中能够 **移动** 的 **最大** 次数。
60+
61+
**示例 1：**
62+
63+
![](https://assets.leetcode.com/uploads/2023/04/11/yetgriddrawio-10.png)
64+
65+
> **输入：** grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
66+
>
67+
> **输出：** 3
68+
>
69+
> **解释：** 可以从单元格 (0, 0) 开始并且按下面的路径移动：
70+
>
71+
> - (0, 0) -> (0, 1).
72+
> - (0, 1) -> (1, 2).
73+
> - (1, 2) -> (2, 3).
74+
>
75+
> 可以证明这是能够移动的最大次数。
76+
77+
**示例 2：**
78+
79+
> ![](https://assets.leetcode.com/uploads/2023/04/12/yetgrid4drawio.png)
80+
>
81+
> **输入：** grid = [[3,2,4],[2,1,9],[1,1,7]]
82+
>
83+
> **输出：** 0
84+
>
85+
> **解释：** 从第一列的任一单元格开始都无法移动。
86+
87+
**提示：**
88+
89+
- `m == grid.length`
90+
- `n == grid[i].length`
91+
- `2 <= m, n <= 1000`
92+
- `4 <= m * n <= 10^5`
93+
- `1 <= grid[i][j] <= 10^6`
94+
95+
## 解题思路
96+
97+
可以使用动态规划来计算从矩阵第一列的任一单元格出发，能够移动的最大次数。
98+
99+
### 思路一：动态规划
100+
101+
1. **初始化状态**：
102+
创建一个 `dp` 数组，其中 `dp[i][j]` 表示从单元格 `(i, j)` 开始能够移动的最大次数。初始时，所有单元格的最大移动次数都设为 `0`，因为矩阵的最后一列没有后续的单元格可移动，移动次数就是 `0`。
103+
104+
2. **倒序遍历列**：
105+
106+
从矩阵的倒数第二列开始遍历，直到第一列。在每一列中，我们都要计算从这一列每个单元格可以向右移动到下一列的次数。
107+
108+
3. **检查可移动条件**：
109+
110+
- 对于每个单元格 `(i, j)`，检查以下三个方向是否满足移动条件：
111+
- 移动到上右 `(i - 1, j + 1)`，如果 `i > 0` 并且 `grid[i][j] < grid[i - 1][j + 1]`，则可以移动，更新移动次数。
112+
- 移动到右 `(i, j + 1)`，如果 `grid[i][j] < grid[i][j + 1]`，则可以移动，更新移动次数。
113+
- 移动到下右 `(i + 1, j + 1)`，如果 `i < m - 1` 并且 `grid[i][j] < grid[i + 1][j + 1]`，则可以移动，更新移动次数。
114+
115+
4. **获取结果**：
116+
- 最后， `dp[i][0]` 中存储的就是从第一列任一单元格出发，能够移动的最大次数，从中获取最大的移动次数，作为结果返回。
117+
118+
#### 复杂度分析
119+
120+
- **时间复杂度**：`O(m * n)`，其中 `m`、`n` 分别是矩阵的行数和列数，需要遍历整个矩阵。
121+
- **空间复杂度**：`O(m * n)`，用于存储 `dp` 数组。
122+
123+
### 思路二：压缩状态的动态规划
124+
125+
1. **初始化状态**：
126+
使用一个一维数组 `dp`，长度为 `m`，表示从每一行的某一列出发，能够到达的最大移动次数。最开始，`dp[i]` 表示从最后一列的第 `i` 行出发时的移动次数，因为没有后续的单元格可移动，初始值为 `0`。
127+
128+
2. **倒序遍历列**：
129+
130+
从矩阵的倒数第二列开始遍历，直到第一列。在每一列中，我们都要计算从这一列每个单元格可以向右移动到下一列的次数。
131+
132+
3. **检查可移动条件**：
133+
134+
- 对于每个单元格 `(i, j)`，检查以下三个方向是否满足移动条件：
135+
- 移动到上右 `(i - 1, j + 1)`，如果 `i > 0` 并且 `grid[i][j] < grid[i - 1][j + 1]`，则可以移动，更新移动次数。
136+
- 移动到右 `(i, j + 1)`，如果 `grid[i][j] < grid[i][j + 1]`，则可以移动，更新移动次数。
137+
- 移动到下右 `(i + 1, j + 1)`，如果 `i < m - 1` 并且 `grid[i][j] < grid[i + 1][j + 1]`，则可以移动，更新移动次数。
138+
139+
4. **更新状态数组**：
140+
141+
- 因为后续计算还依赖下一列的移动次数，所以需要通过临时数组 `newDp` 存储当前列的移动次数，在遍历完当前列后，更新 `dp` 为 `newDp`。
142+
143+
5. **获取结果**：
144+
- 最后， `dp` 数组中存储的就是从第一列任一单元格出发，能够移动的最大次数，从 `dp` 数组中获取最大的移动次数，作为结果返回。
145+
146+
#### 复杂度分析
147+
148+
- **时间复杂度**：`O(m * n)`，其中 `m`、`n` 分别是矩阵的行数和列数，需要遍历整个矩阵。
149+
- **空间复杂度**：`O(m)`，只需要一个一维数组 `dp` 存储状态。
150+
151+
## 代码
152+
153+
::: code-tabs
154+
@tab 动态规划
155+
156+
```javascript
157+
/**
158+
* @param {number[][]} grid
159+
* @return {number}
160+
*/
161+
var maxMoves = function (grid) {
162+
const m = grid.length,
163+
n = grid[0].length;
164+
// 创建 dp 数组
165+
const dp = new Array(m).fill(0).map((i) => new Array(n).fill(0));
166+
167+
// 倒序遍历列
168+
for (let j = n - 2; j >= 0; j--) {
169+
for (let i = 0; i < m; i++) {
170+
// 检查上右、右、下右三个方向
171+
if (i > 0 && grid[i][j] < grid[i - 1][j + 1]) {
172+
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j + 1] + 1);
173+
}
174+
if (grid[i][j] < grid[i][j + 1]) {
175+
dp[i][j] = Math.max(dp[i][j], dp[i][j + 1] + 1);
176+
}
177+
if (i < m - 1 && grid[i][j] < grid[i + 1][j + 1]) {
178+
dp[i][j] = Math.max(dp[i][j], dp[i + 1][j + 1] + 1);
179+
}
180+
}
181+
}
182+
// 获取结果
183+
let maxMoves = 0;
184+
for (let i = 0; i < m; i++) {
185+
maxMoves = Math.max(maxMoves, dp[i][0]);
186+
}
187+
return maxMoves;
188+
};
189+
```
190+
191+
@tab 压缩状态的动态规划
192+
193+
```javascript
194+
/**
195+
* @param {number[][]} grid
196+
* @return {number}
197+
*/
198+
var maxMoves = function (grid) {
199+
const m = grid.length,
200+
n = grid[0].length;
201+
// 初始化 dp 数组
202+
let dp = new Array(m).fill(0);
203+
204+
for (let j = n - 2; j >= 0; j--) {
205+
// 记录当前列的 dp 数组
206+
let newDp = [];
207+
for (let i = 0; i < m; i++) {
208+
// 当前单元格的移动次数
209+
let moves = 0;
210+
// 检查三个可移动方向
211+
if (i > 0 && grid[i][j] < grid[i - 1][j + 1]) {
212+
moves = Math.max(moves, dp[i - 1] + 1);
213+
}
214+
if (grid[i][j] < grid[i][j + 1]) {
215+
moves = Math.max(moves, dp[i] + 1);
216+
}
217+
if (i < m - 1 && grid[i][j] < grid[i + 1][j + 1]) {
218+
moves = Math.max(moves, dp[i + 1] + 1);
219+
}
220+
// 更新当前列的移动次数
221+
newDp.push(moves);
222+
}
223+
// 更新 dp 数组
224+
dp = newDp;
225+
}
226+
// 返回最大的移动次数
227+
return Math.max(...dp);
228+
};
229+
```
230+
231+
:::

‎src/problem/README.md‎

Lines changed: 2 additions & 1 deletion
Original file line numberDiff line numberDiff line change
@@ -1,6 +1,6 @@
11
# 目录
22

3-
已完成 419 道
3+
已完成 420 道
44

55
<!-- prettier-ignore -->
66
| 题号 | 标题 | 题解 | 标签 | 难度 |
@@ -404,6 +404,7 @@
404404
| 2675 | [将对象数组转换为矩阵 🔒](https://leetcode.com/problems/array-of-objects-to-matrix) | [[✓]](/problem/2675.md) | | <font color=#ff334b>Hard</font> |
405405
| 2676 | [节流 🔒](https://leetcode.com/problems/throttle) | [[✓]](/problem/2676.md) | | <font color=#ffb800>Medium</font> |
406406
| 2677 | [分块数组](https://leetcode.com/problems/chunk-array) | [[✓]](/problem/2677.md) | | <font color=#15bd66>Easy</font> |
407+
| 2684 | [矩阵中移动的最大次数](https://leetcode.com/problems/maximum-number-of-moves-in-a-grid) | [[✓]](/problem/2684.md) | [`数组`](/tag/array.md) [`动态规划`](/tag/dynamic-programming.md) [`矩阵`](/tag/matrix.md) | <font color=#ffb800>Medium</font> |
407408
| 2694 | [事件发射器](https://leetcode.com/problems/event-emitter) | [[✓]](/problem/2694.md) | | <font color=#ffb800>Medium</font> |
408409
| 2695 | [包装数组](https://leetcode.com/problems/array-wrapper) | [[✓]](/problem/2695.md) | | <font color=#15bd66>Easy</font> |
409410
| 2696 | [删除子串后的字符串最小长度](https://leetcode.com/problems/minimum-string-length-after-removing-substrings) | [[✓]](/problem/2696.md) | [`栈`](/tag/stack.md) [`字符串`](/tag/string.md) [`模拟`](/tag/simulation.md) | <font color=#15bd66>Easy</font> |

‎src/tag/array.md‎

Lines changed: 1 addition & 1 deletion
Original file line numberDiff line numberDiff line change
@@ -1426,7 +1426,7 @@
14261426
| 2681 | [英雄的力量](https://leetcode.com/problems/power-of-heroes) | | [`数组`](/tag/array.md) [`数学`](/tag/math.md) [`动态规划`](/tag/dynamic-programming.md) `2+` | <font color=#ff334b>Hard</font> |
14271427
| 2682 | [找出转圈游戏输家](https://leetcode.com/problems/find-the-losers-of-the-circular-game) | | [`数组`](/tag/array.md) [`哈希表`](/tag/hash-table.md) [`模拟`](/tag/simulation.md) | <font color=#15bd66>Easy</font> |
14281428
| 2683 | [相邻值的按位异或](https://leetcode.com/problems/neighboring-bitwise-xor) | | [`位运算`](/tag/bit-manipulation.md) [`数组`](/tag/array.md) | <font color=#ffb800>Medium</font> |
1429-
| 2684 | [矩阵中移动的最大次数](https://leetcode.com/problems/maximum-number-of-moves-in-a-grid) | | [`数组`](/tag/array.md) [`动态规划`](/tag/dynamic-programming.md) [`矩阵`](/tag/matrix.md) | <font color=#ffb800>Medium</font> |
1429+
| 2684 | [矩阵中移动的最大次数](https://leetcode.com/problems/maximum-number-of-moves-in-a-grid) | [[✓]](/problem/2684.md) | [`数组`](/tag/array.md) [`动态规划`](/tag/dynamic-programming.md) [`矩阵`](/tag/matrix.md) | <font color=#ffb800>Medium</font> |
14301430
| 2702 | [使数字变为非正数的最小操作次数 🔒](https://leetcode.com/problems/minimum-operations-to-make-numbers-non-positive) | | [`数组`](/tag/array.md) [`二分查找`](/tag/binary-search.md) | <font color=#ff334b>Hard</font> |
14311431
| 2706 | [购买两块巧克力](https://leetcode.com/problems/buy-two-chocolates) | | [`贪心`](/tag/greedy.md) [`数组`](/tag/array.md) [`排序`](/tag/sorting.md) | <font color=#15bd66>Easy</font> |
14321432
| 2707 | [字符串中的额外字符](https://leetcode.com/problems/extra-characters-in-a-string) | | [`字典树`](/tag/trie.md) [`数组`](/tag/array.md) [`哈希表`](/tag/hash-table.md) `2+` | <font color=#ffb800>Medium</font> |

0 commit comments

Comments
 (0)